領域上の最適化
領域制約を使って制約された最適化問題を解く．領域制約は領域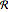 
に対して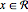 
を使って表され，それだけででも，他の制約と一緒にでも使うことができる．記号的な最適化関数だけでなく局所的および大域的な数値的最適化関数もこれらの新しい制約条件をサポートする．
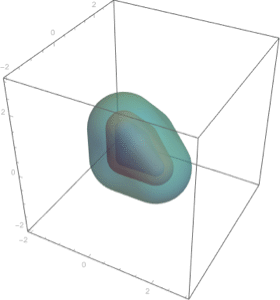
円板上で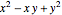
を最小および最大にする点を求める．
| In[1]:= |  X |
| Out[1]= |  |
| In[2]:= |  X |
| Out[2]= |  |
| In[3]:= |  X |
| Out[3]= |  |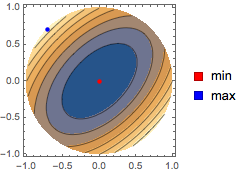
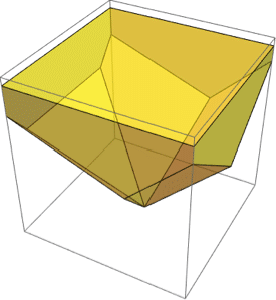
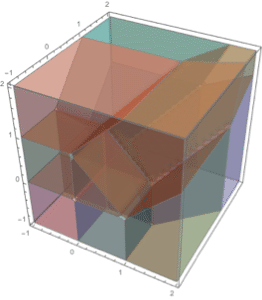
2つの領域間で最短距離および最長距離となる点のペアを求める．
| In[4]:= |  X |
| In[5]:= |  X |
| Out[5]= |  |
| In[6]:= |  X |
| Out[6]= |  |
| In[7]:= |  X |
| Out[7]= |  |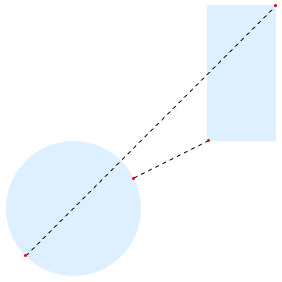
最短距離と最長距離となる点を厳密に求める．
| In[8]:= |  X |
| In[9]:= |  X |
| Out[9]= |  |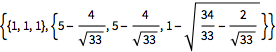
| In[10]:= |  X |
| Out[10]= |  |
| In[11]:= |  X |
| Out[11]= |  |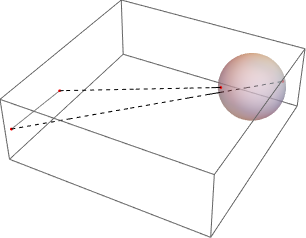
