Números primos de Mersenne y números perfectos

Un primo de Mersenne es un número primo de la forma 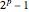, donde el exponente primo de Mersenne 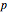es también un número primo. Cada primo de Mersenne corresponde a un número perfecto par.

Genere una lista de exponentes primos de Mersenne.

In[1]:=

mpe = Table[MersennePrimeExponent[n], {n, 1, 10}]

Out[1]=

Construya los correspondientes números primos de Mersenne.

In[2]:=

mp = 2^mpe - 1

Out[2]=

Construya los correspondientes números perfectos.

In[3]:=

pn = 2^(mpe - 1) (2^mpe - 1)

Out[3]=

In[4]:=

AllTrue[pn, PerfectNumberQ]

Out[4]=

Visualice qué tan escasa es la distribución de pequeños exponentes primos de Mersenne enfatizándolos en rojo en la lista de los primeros 225 números primos.

In[5]:=

primes = Replace[Prime@Range[225], x_?MersennePrimeExponentQ :> Style[x, Red, Bold], 1];

In[6]:=

Multicolumn[primes, Alignment -> {Center, Center}, Spacings -> {1, 1}, Frame -> All, FrameStyle -> Directive[Orange, Dashing[Small]]]

Out[6]=