Representaciones de números complejos

Las nuevas funciones ReIm y AbsArg facilitan la conversión de números complejos a su representación cartesiana o polar.

Convierta un número complejo 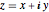al par ordenado .

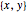In[1]:=

ReIm[3 + 4 I]

Out[1]=

Convierta varios números.

In[2]:=

ReIm[{Pi, -2 I, Sqrt[-I], 3 Exp[I 2 Pi/3]}]

Out[2]=

Convierta a un número complejo 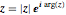al par ordenado .

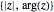In[3]:=

AbsArg[3 + 4 I]

Out[3]=

Convierta a varios números.

In[4]:=

AbsArg[{Pi, -2 I, Sqrt[-I], 3 Exp[I 2 Pi/3]}]

Out[4]=

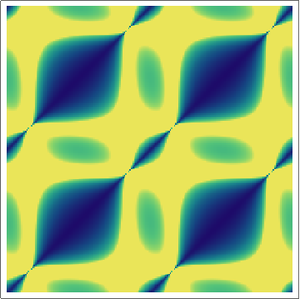
Represente gráficamente una función compleja como una curva en el plano complejo.

In[5]:=

ParametricPlot[ReIm[(-2)^x], {x, 0, 4}]

Out[5]=

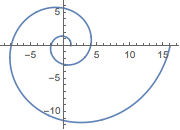
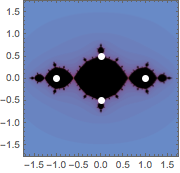
Anote puntos complejos en un gráfico de plano complejo.

In[6]:=

JuliaSetPlot[-1, PlotRange -> 1.75, Epilog -> {PointSize[Large], White, Point[ReIm[{I/2, -I/2, 1, -1}]]}]

Out[6]=