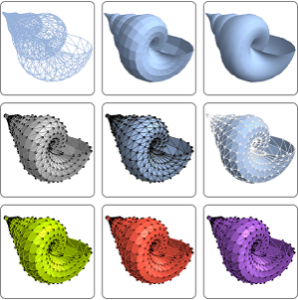
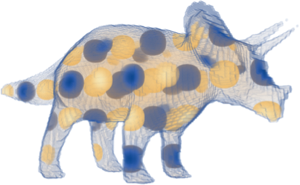
Уравнения в частных производных для геометрических объектов
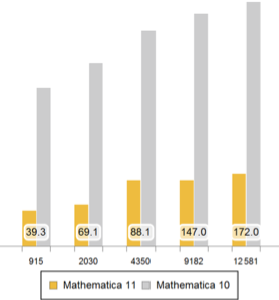
Версия 11 добавляет расширенную поддержку символических и численных решений краевых задач над регионами.
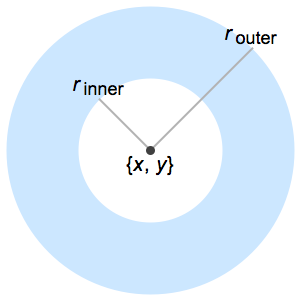
В данном примере приведена задача Дирихле для уравнения Лапласа в круге.
In[1]:=
leqn = Laplacian[u[x, y],{x, y}] == 0;In[2]:=
dcond = DirichletCondition[u[x, y] == Sin[6 ArcTan[y/x]], True]; In[3]:=
\[CapitalOmega] = Disk[{0, 0}, 3];Решим уравнение 
на единичном круге с граничным условием Дирихле.
In[4]:=
sol = DSolveValue[{leqn, dcond},
u[x, y], {x, y} \[Element] \[CapitalOmega]]Out[4]=
In[5]:=
Plot3D[sol, {x, y} \[Element] \[CapitalOmega], PlotRange -> All,
PlotStyle -> Hue[0.5], Exclusions -> None]Out[5]=
