Wolfram言語™

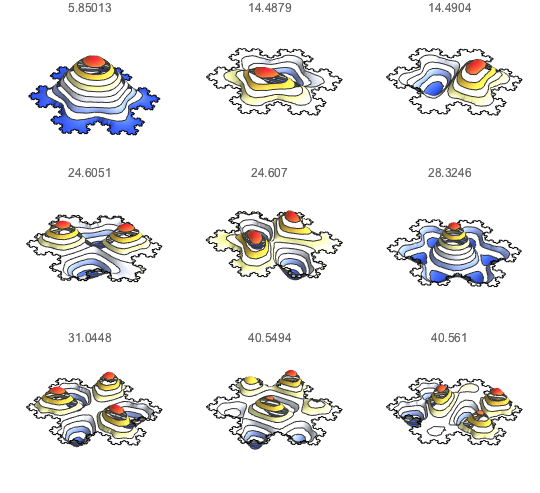
コッホ(Koch)雪片のスペクトルを計算する

再帰的コッホ雪片を生成する．

In[1]:=

KochStep[{p1_, p2_}] := With[{q1 = p1 + (p2 - p1)/3, q3 = p1 + 2 (p2 - p1)/3, q2 = (p1 + (p2 - p1)/3) + RotationMatrix[-\[Pi]/3].(p2 - p1)/3}, {p1, q1, q2, q3, p2}]; KochStep[pp : {{_, _} ..}] := Join[Partition[Flatten[Most /@ (KochStep /@ Partition[pp, 2, 1])], 2], {pp[[-1]]}]; vertices = Nest[KochStep, N[{{3 Sqrt[3]/4, 3/4}, {-3 Sqrt[3]/4, 3/4}, {0, -3/2}, {3 Sqrt[3]/4, 3/4}}], 4]; region = Polygon[vertices];

ラプラス演算子を指定する．

In[2]:=

\[ScriptCapitalL] = -Laplacian[u[x, y], {x, y}];

ディリクレ境界条件を指定する．

In[3]:=

\[ScriptCapitalB] = DirichletCondition[u[x, y] == 0, True];

ラプラス演算子の固有値と固有関数を9個計算する．

In[4]:=

{vals, funs} = NDEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, u[x, y], {x, y} \[Element] region, 9];

固有値を調べる．

In[5]:=

vals

Out[5]=

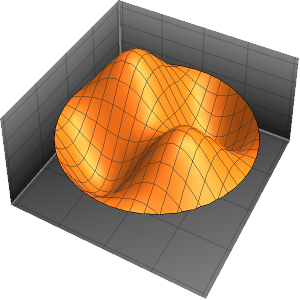
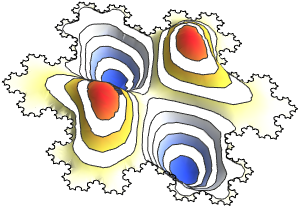
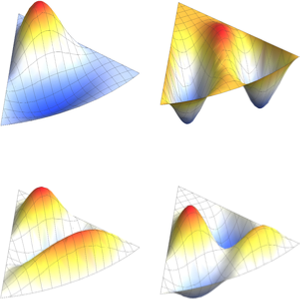
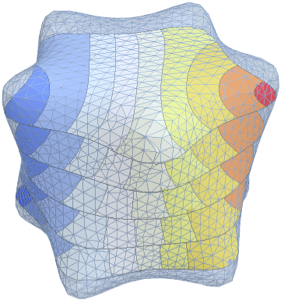
固有関数を可視化する．

In[6]:=

Grid[Partition[ Table[Plot3D[funs[[i]], {x, y} \[Element] region, PlotLabel -> vals[[i]], MeshFunctions -> {#3 &}, MeshShading -> {Automatic, None}, Mesh -> 10, Background -> None, Boxed -> False, Axes -> None, PlotRange -> All, ColorFunction -> "TemperatureMap"], {i, Length[vals]}], 3], Spacings -> 0]

Out[6]=