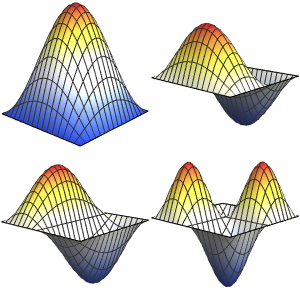
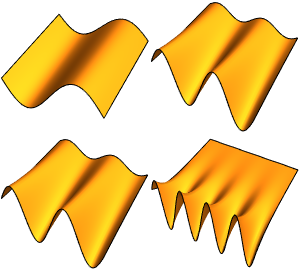
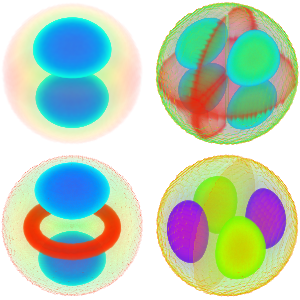
球体に含まれるラプラス演算子の固有関数のギャラリーを作成する

3Dラプラス演算子を定義する．

In[1]:=

\[ScriptCapitalL] = -Laplacian[u[x, y, z], {x, y, z}];

同次ディリクレ境界条件を指定する．

In[2]:=

\[ScriptCapitalB] = DirichletCondition[u[x, y, z] == 0, True];

球体の中の固有値と固有関数を小さい方から16個求める．

In[3]:=

\[CapitalOmega] = Ball[{0, 0, 0}, 2];

In[4]:=

{vals, funs} = DEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, u[x, y, z], {x, y, z} \[Element] \[CapitalOmega], 16];

固有値はBesselJZeroで与えられる．

In[5]:=

vals[[1]] // TraditionalForm

Out[5]//TraditionalForm=

固有関数のギャラリーを生成する．

In[6]:=

Grid[Partition[ ParallelTable[ DensityPlot3D[ funs[[i]] // N // Evaluate, {x, y, z} \[Element] \[CapitalOmega], Boxed -> False, Axes -> False, ColorFunction -> Hue, Method -> {"ShrinkWrap" -> True}, ImageSize -> 125], {i, 16}], 4]]

Out[6]=