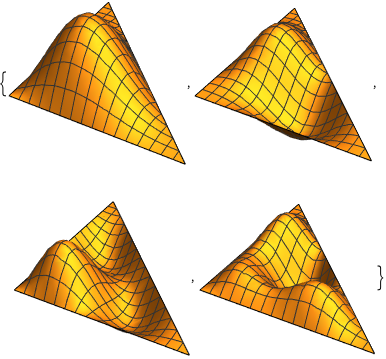Символические собственные функции в треугольных мембранах
Укажем оператор Лапласа.
In[1]:=
\[ScriptCapitalL] = -Laplacian[u[x, y], {x, y}];Укажем однородные граничные условия Дирихле.
In[2]:=
\[ScriptCapitalB] = DirichletCondition[u[x, y] == 0, True];Найдем четыре наименьших собственные значения и собственные функции оператора в треугольнике.
In[3]:=
{vals, funs} =
DEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]},
u[x, y], {x, y} \[Element] Triangle[], 4];In[4]:=
valsOut[4]=
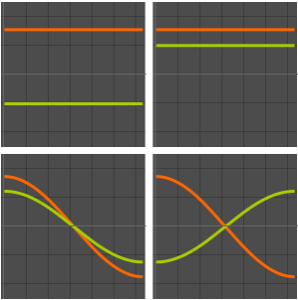
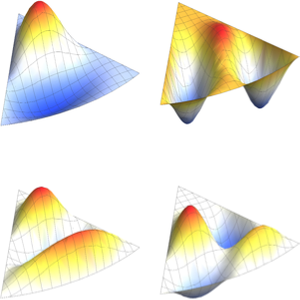
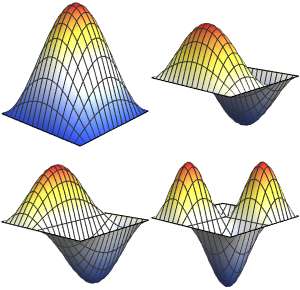
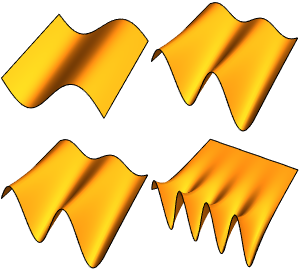
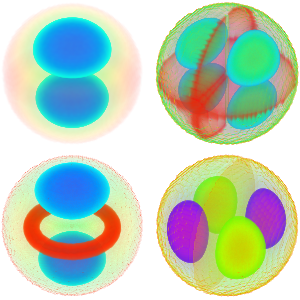
Визуализируем собственные функции.
In[5]:=
Table[Plot3D[funs[[i]], {x, y} \[Element] Triangle[], Boxed -> False,
Axes -> False, Method -> {"ShrinkWrap" -> True}], {i, 4}]Out[5]=