Прогноз собственных значений волнового оператора
Найти четыре наименьших собственных значения и собственных функции обобщенного волнового уравнения  .
.
Настроим общий волновой оператор для  .
.
In[1]:=
\[Gamma] = 1.3; c = 1.1;
op = D[u[t, x], {t, 2}] + \[Gamma] D[u[t, x], {t, 1}] -
c^2 D[u[t, x], {x, 2}] + \[Gamma] u[t, x];Найдем четыре наименьших собственных значения и собственных функции в 1-мерном пространстве.
In[2]:=
{vals, funs} = NDEigensystem[op == 0, u[t, x], t, {x, 0, \[Pi]}, 4];Рассмотрим полученные собственные значения.
In[3]:=
valsOut[3]=
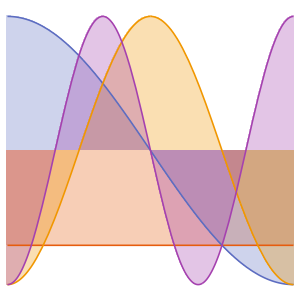
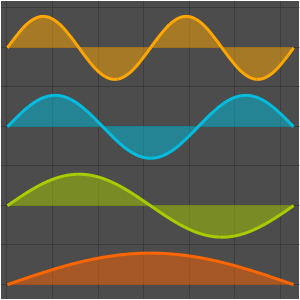
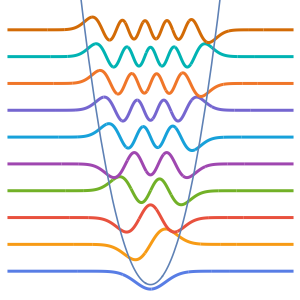
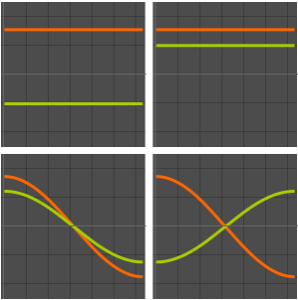
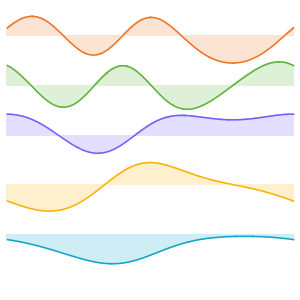
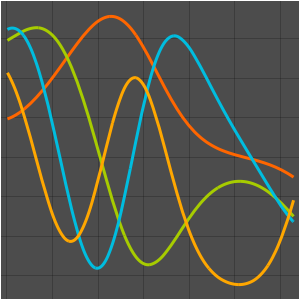
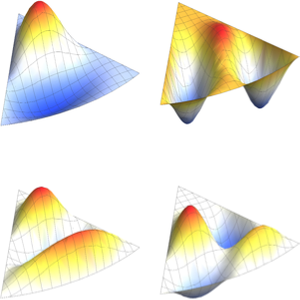
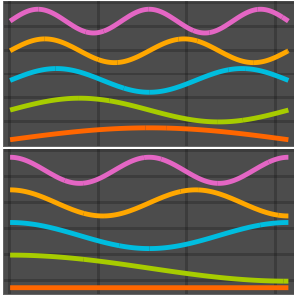
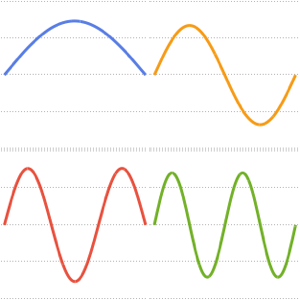
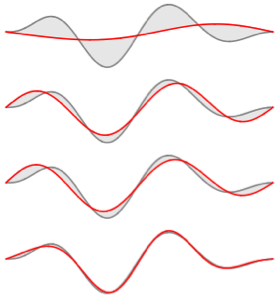
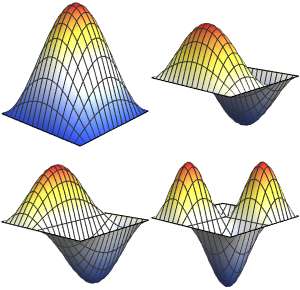
Визуализируем действительные и мнимые части собственных функций. Обратим внимание на то, что собственные функции, как и собственные значения, находятся в сопряженных парах.
In[4]:=

Grid[Partition[
Plot[Evaluate[ReIm[#]], {x, 0, \[Pi]}, PlotRange -> .5,
PlotLegends -> {HoldForm@Re[f], HoldForm@Im[f]}] & /@ funs, 2]]Out[4]=