Язык Wolfram Language™

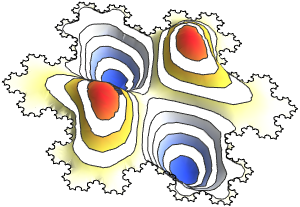
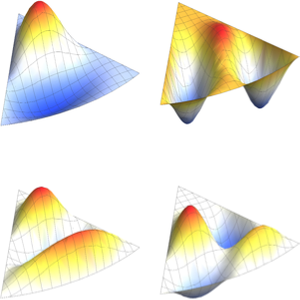
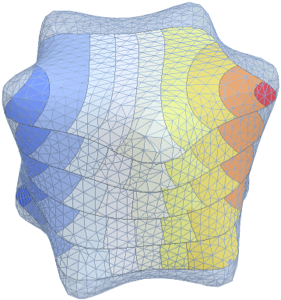
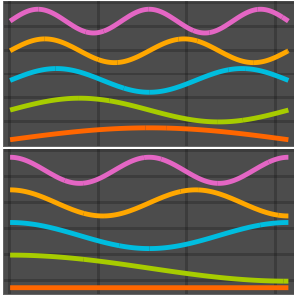
Одномерные символьные собственные функции лапласиана

Укажем одномерный лапласовский оператор.

In[1]:=

\[ScriptCapitalL] = -Laplacian[u[x], {x}];

Укажем однородные граничные условия Дирихле для собственных функций.

In[2]:=

\[ScriptCapitalB]1 = DirichletCondition[u[x] == 0, True];

Определим пять наименьших собственных значений и собственных функций.

In[3]:=

{vals, funs} = DEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]1}, u[x], {x, 0, \[Pi]}, 5];

Проверим полученные собственные значения.

In[4]:=

vals

Out[4]=

Проверим полученные собственные функции.

In[5]:=

funs

Out[5]=

Визуализируем полученные собственные функции.

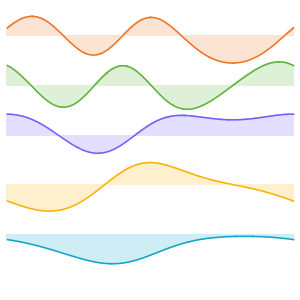
In[6]:=

Plot[Evaluate[funs + 2 Range[5]], {x, 0, \[Pi]}]

Out[6]=

Укажем однородное граничное условие Неймана.

In[7]:=

\[ScriptCapitalB]2 = NeumannValue[0, True];

Найдем пять наименьших собственных значений и собственных функций.

In[8]:=

{vals, funs} = DEigensystem[\[ScriptCapitalL] + \[ScriptCapitalB]2, u[x], {x, 0, \[Pi]}, 5];

Проверим полученные собственные значения. Относительно условий Дирихле был добавлен нулевой режим.

In[9]:=

vals

Out[9]=

Косинусы были заменены на синусы в полученных собственных функциях.

In[10]:=

funs

Out[10]=

Визуализируем собственные функции.

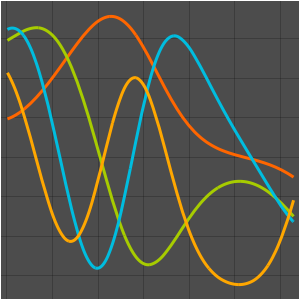
In[11]:=

Plot[Evaluate[funs + 2 Range[5]], {x, 0, \[Pi]}]

Out[11]=