Определение символических собственных значений

Укажем одномерный лапласовский оператор.

In[1]:=

\[ScriptCapitalL] = -Laplacian[u[x], {x}];

Зададим однородное граничное условие Дирихле.

In[2]:=

\[ScriptCapitalB] = DirichletCondition[u[x] == 0, True];

Найдем выражения для 5 самых маленьких собственных значений на отрезке .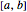

In[3]:=

DEigenvalues[{\[ScriptCapitalL], \[ScriptCapitalB]}, u[x], {x, a, b}, 5]

Out[3]=

Укажем оператор Эйри.

In[4]:=

\[ScriptCapitalL] = -Laplacian[u[x], {x}] + x u[x];

Найдем 5 наименьших собственных значений и соответствующих собственных функций.

In[5]:=

{vals, funs} = DEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, u[x], {x, 0, 1}, 5];

Собственные значения представляют собой корни трансцендентного уравнения.

In[6]:=

vals[[1]] // TraditionalForm

Out[6]//TraditionalForm=

С точностью определим трансцендентальное собственное значение.

In[7]:=

N[vals[[1]], 500] // TraditionalForm

Out[7]//TraditionalForm=

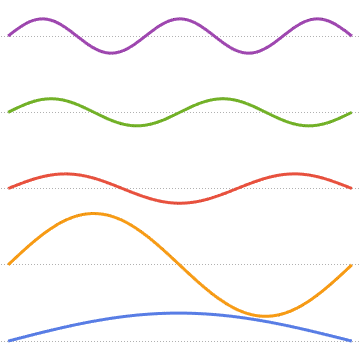
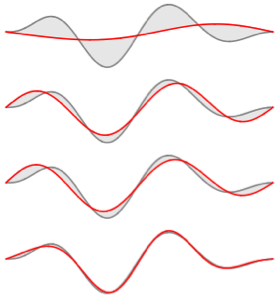
Визуализируем собственные функции.

In[8]:=

Plot[Evaluate[funs + Range[5]], {x, 0, 1}, ImageSize -> Medium, PlotTheme -> {"Business", "Bare"}, AspectRatio -> 1]

Out[8]=