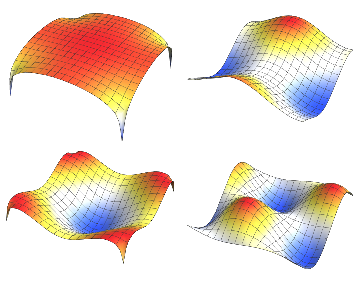Анализ уравнения Лапласа на торе

Найдем пять наименьших собственных значений и собственных функций уравнения Лапласа на квадратном торе с ограничением Дирихле.

Укажем периодические граничные условия на квадрат с длинной =1.

In[1]:=

torusBCs = {u[0, y] == u[1, y], u[x, 0] == u[x, 1]};

Укажем значение в начале координат. При периодических условиях, данное значение должно быть соблюдено и в остальных трех углах квадрата.

In[2]:=

constraint = DirichletCondition[u[x, y] == 0, x == 0 && y == 0];

Вычислим собственные значения и собственные функции.

In[3]:=

{vals, funs} = NDEigensystem[ Join[{-Laplacian[u[x, y], {x, y}], constraint}, torusBCs], u[x, y], {x, y} \[Element] Rectangle[{0, 0}, {1, 1}], 4];

Рассмотрим полученные собственные значения.

In[4]:=

vals

Out[4]=

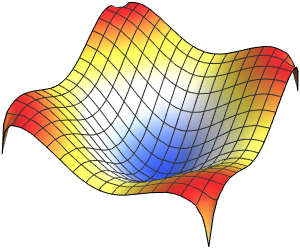
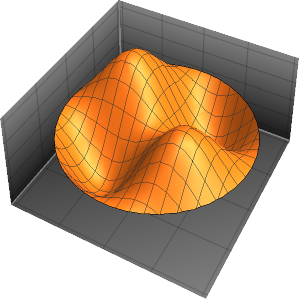
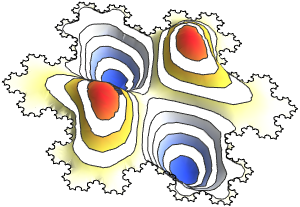
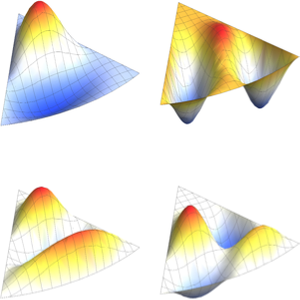
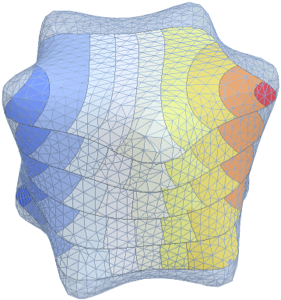
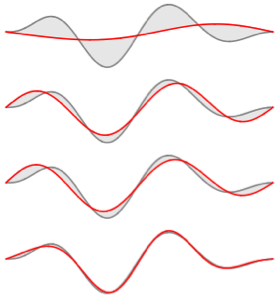
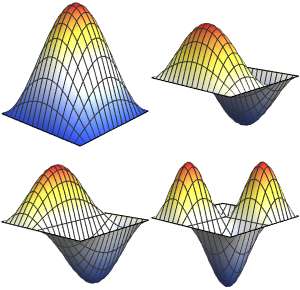
Визуализируем полученные собственные функции.

In[5]:=

ImageCollage[ Plot3D[#, {x, y} \[Element] Rectangle[{0, 0}, {1, 1}], ColorFunction -> "TemperatureMap", Boxed -> False, Axes -> None, PlotRange -> All, PlotStyle -> {Specularity[White, 20]}] & /@ funs, Background -> Transparent]

Out[5]=