Análisis de datos de enfermedades cardíacas
El análisis de datos es un proceso de extracción, presentación y modelado basado en información extraída de fuentes primarias. En este ejemplo, se muestra un flujo de trabajo de análisis de datos en Wolfram Language. El conjunto de datos utilizado aquí proviene del repositorio UCI Machine Learning Repository, el cual consiste en datos de diagnósticos de enfermedades cardíacas en 1.541 pacientes.
Importe los datos de diagnóstico de enfermedades cardíacas y segméntelos, con el fin de que las filas correspondan con distintos pacientes, y las columnas correspondan con distintas propiedades.
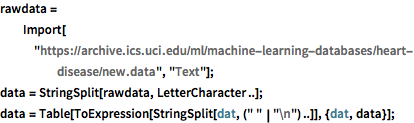
rawdata =
Import["https://archive.ics.uci.edu/ml/machine-learning-databases/\
heart-disease/new.data", "Text"];
data = StringSplit[rawdata, LetterCharacter ..];
data = Table[
ToExpression[StringSplit[dat, (" " | "\n") ..]], {dat, data}];Extraiga las propiedades relevantes como "etiquetas" y "propiedades". Los valores almacenados en "etiquetas" son 0 y 1, los cuales corresponden a la presencia u ausencia de enfermedades cardíacas, respectivamente.
labels = Unitize[data[[All, 58]]];
features =
data[[All, {3, 4, 9, 10, 12, 16, 19, 32, 38, 40, 41, 44, 51}]];Take[labels, 10]Para cada paciente, el vector propiedad es una lista de valores numéricos. Sin embargo, los datos no están completos y posee campos faltantes almacenados como 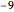 .
.
features[[-3]]Remplace los valores faltantes por el promedio de los datos disponibles en el atributo correspondiente, luego visualice la correlación entre distintos atributos.

features = Transpose[Table[
N[attribute /. {-9 -> Mean[N[DeleteCases[attribute, -9]]]}]
, {attribute, Transpose[features]}]];
cormat = Correlation[features];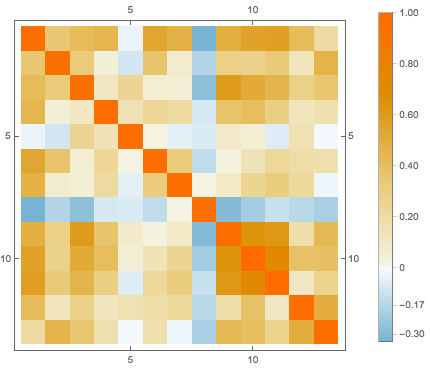
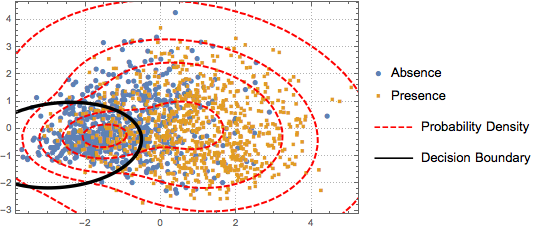
Para visualizar la distribución de los datos, se realiza PCA para extraer los primeros dos componentes principales, luego los datos proyectados son presentados en un gráfico de dispersión.
pcs2 = Take[PrincipalComponents[features, Method -> "Correlation"],
All, 2];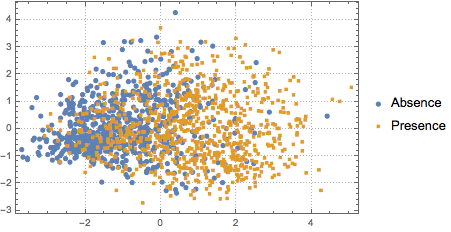
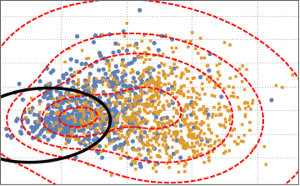
Para distinguir las dos clases, los datos proyectados son ajustados en un modelo gaussiano mixto de dos componentes.

edist = EstimatedDistribution[pcs2,
MixtureDistribution[{p1,
p2}, {BinormalDistribution[{m11, m12}, {s11, s12}, r1],
BinormalDistribution[{m21, m22}, {s21, s22}, r2]}]];Con base en el modelo mixto, grafique los límites de decisión (curva negra) y los contornos de densidad de probabilidad (curva roja) del modelo mixto, y muéstrelos junto con el gráfico de dispersión. El primer componente de la mezcla gaussiana tiene mayor probabilidad dentro del límite de decisión.