‹›Probabilidad y estadística extendidasEstimación de distribución más rápida
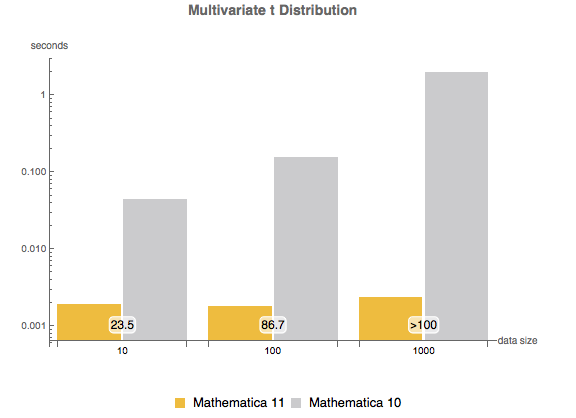
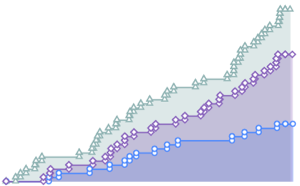
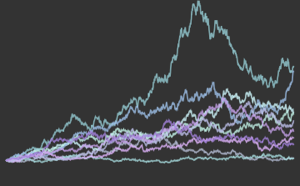
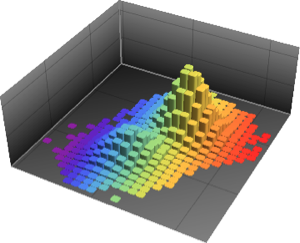
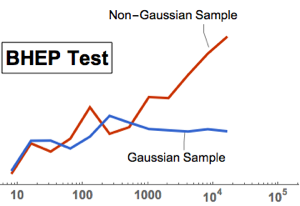
La versión 11 agrega numerosas mejoras para la estimación de distribución, especialmente en rendimiento. Los siguiente cuadros muestran los tiempos de estimación de varias distribuciones con distintos tamaños de muestra. Los experimentos fueron realizados en un sistema de Windows 10 con un procesador Intel Xeon E3-1245 v2 3.40 GHz. El número en la parte inferior muestra cuán rápida es la versión 11 comparada con la versión 10.
Distribución 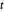 de Student.
de Student.
muestre la entrada completa de Wolfram Language
dist = StudentTDistribution[loc, sc, df];
ndist = StudentTDistribution[-1, 1, 2];
Table[
sample = BlockRandom[SeedRandom["MarketingExample"];
RandomVariate[ndist, n]];
Mean[Table[
First[AbsoluteTiming[EstimatedDistribution[sample, dist];]], {5}]]
, {n, {10, 100, 1000}}]
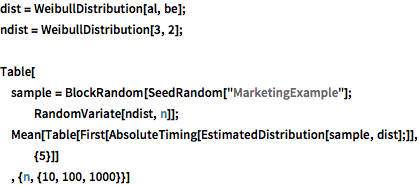
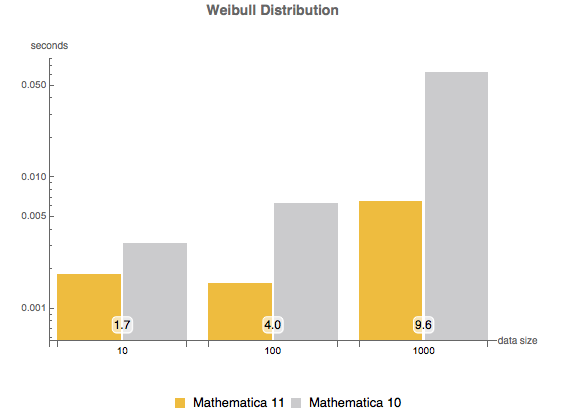
Distribución de Weibull.
muestre la entrada completa de Wolfram Language
dist = WeibullDistribution[al, be];
ndist = WeibullDistribution[3, 2];
Table[
sample = BlockRandom[SeedRandom["MarketingExample"];
RandomVariate[ndist, n]];
Mean[Table[
First[AbsoluteTiming[EstimatedDistribution[sample, dist];]], {5}]]
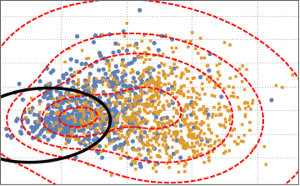
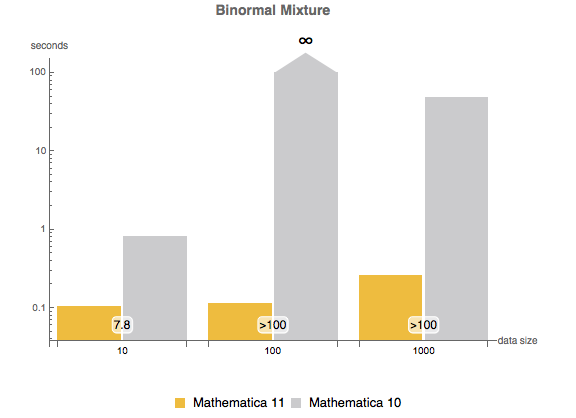
, {n, {10, 100, 1000}}]Mezcla de distribuciones binormales.
muestre la entrada completa de Wolfram Language
dist = MixtureDistribution[{w1,
w2}, {BinormalDistribution[{m11, m12}, {s11, s12}, \[Rho]1],
BinormalDistribution[{m21, m22}, {s21, s22}, \[Rho]2]}];
ndist = MixtureDistribution[{0.3,
0.7}, {BinormalDistribution[{0, 1}, {0.5, 0.25}, 0.7],
BinormalDistribution[{-0.5, 0}, {0.5, 0.25}, 0.1]}];
Table[
sample = BlockRandom[SeedRandom["MarketingExample"];
RandomVariate[ndist, n]];
Mean[Table[
First[AbsoluteTiming[
TimeConstrained[EstimatedDistribution[sample, dist];,
100]]], {5}]]
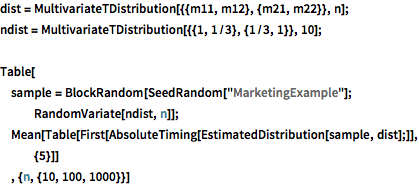
, {n, {10, 100, 1000}}]Distribución 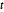 multivariable.
multivariable.
muestre la entrada completa de Wolfram Language
dist = MultivariateTDistribution[{{m11, m12}, {m21, m22}}, n];
ndist = MultivariateTDistribution[{{1, 1/3}, {1/3, 1}}, 10];
Table[
sample = BlockRandom[SeedRandom["MarketingExample"];
RandomVariate[ndist, n]];
Mean[Table[
First[AbsoluteTiming[EstimatedDistribution[sample, dist];]], {5}]]
, {n, {10, 100, 1000}}]
 de Student.
de Student.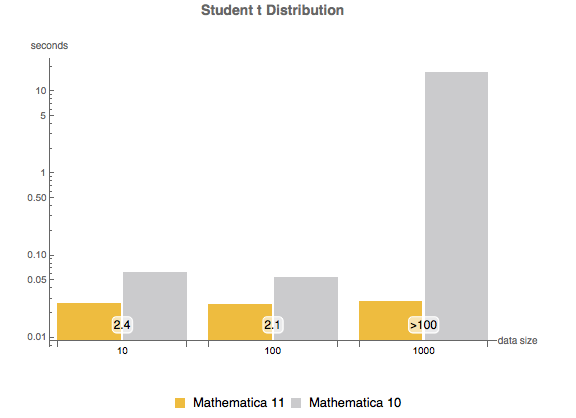
 multivariable.
multivariable.