Wolfram Language™

Proceso de Poisson no homogéneo

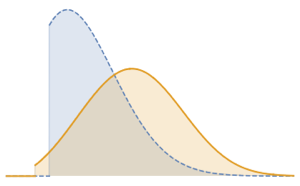
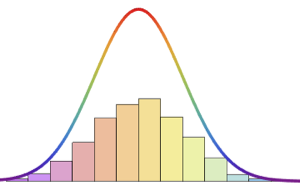
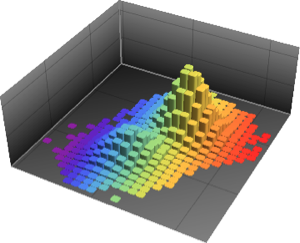
Un proceso de Poisson no homogéneo es un proceso con una tasa de tiempo variable. Puede ser usado para modelar los tiempos de llegada de clientes a una tienda, eventos de tránsito y posiciones de daño a lo largo de una carretera. La densidad de probabilidad del proceso en cualquier porción temporal t es una distribución de Poisson.

In[1]:=

PDF[InhomogeneousPoissonProcess[f[\[Tau]], \[Tau]][t], x]

Out[1]=

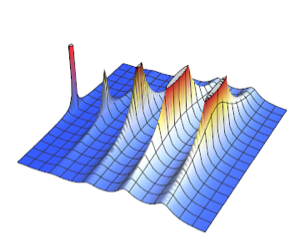
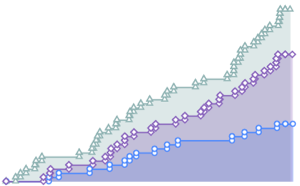
Simule un proceso de Poisson no homogéneo.

In[2]:=

td = RandomFunction[ InhomogeneousPoissonProcess[2 + 1/(1 + t^2), t], {0, 20}];

In[3]:=

ListStepPlot[td, Filling -> Axis, ImageSize -> Medium, PlotTheme -> "Detailed"]

Out[3]=

Un proceso de Poisson no homogéneo puede ser usado para modelar cuentas de llegada. Aquí, el proceso es usado para simular el número de llegadas en un pequeño restaurante de comidas rápidas si las tasas de llegadas de clientes por hora son dadas.

In[4]:=

arrivalrates = {{0, 8}, {1, 9}, {2, 7}, {4, 6}, {5, 12}, {6, 14}, {7, 11}, {8, 6}, {9, 4}, {10, 3}, {11, 8}, {12, 15}, {13, 12}, {14, 10}, {15, 8}, {16, 6}, {17, 12}, {18, 17}, {19, 15}, {20, 12}, {21, 6}, {22, 5}, {23, 7}}; \[Lambda][t_] = Interpolation[arrivalrates, InterpolationOrder -> 1][t];

In[5]:=

Plot[\[Lambda][t], {t, 0, 23}, Exclusions -> None, Filling -> Axis, ImageSize -> Medium, PlotTheme -> "Detailed"]

Out[5]=

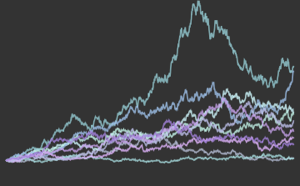
Defina un proceso de Poisson no homogéneo para las llegadas con base en la función de tasa dada λ(t) y simule las cuentas de llegadas en un día.

In[6]:=

\[ScriptCapitalP] = InhomogeneousPoissonProcess[\[Lambda][t], t]; td = RandomFunction[\[ScriptCapitalP], {0, 23, 1}, 3];

In[7]:=

ListStepPlot[td, ImageSize -> Medium, PlotTheme -> "Detailed"]

Out[7]=