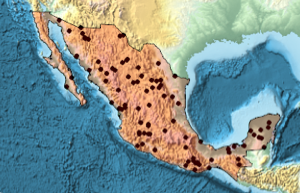
Muestra de un proceso de puntos de Poisson

Un proceso de puntos de Poisson es una generalización de un proceso unidimensional de Poisson de un caso multi-dimensional. Un proceso de puntos de Poisson homogéneo en regiones geométricas puede ser muestreado usando RandomPoint.

Cree un polígono de país.

In[1]:=

region = DiscretizeGraphics[CountryData["Mexico", "Polygon"], ImageSize -> Medium]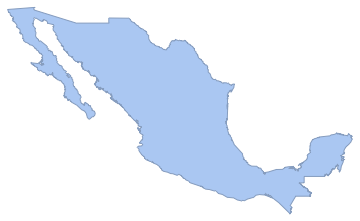

Out[1]=

Defina una función que muestree un proceso de puntos de Poisson con tres argumentos: región, intensidad y número de realizaciones.

In[2]:=

ppp[region_, intensity_, n_] := Module[{nlist, pts}, nlist = RandomVariate[PoissonDistribution[intensity RegionMeasure[region]], n]; pts = RandomPoint[region, Total[nlist]]; nlist = Accumulate[nlist]; nlist = Transpose[{Prepend[Most[nlist] + 1, 1], nlist}]; Table[Take[pts, ind], {ind, nlist}] ]

Genere una realización de un proceso de puntos de Poisson en el polígono de país con intensidad 0.5 y visualícelo con Graphics.

In[3]:=

intensity = 0.5; sample = ppp[region, intensity, 1];

In[4]:=

Show[region, Graphics[{Black, Point @@ sample}]]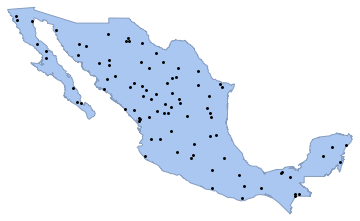

Out[4]=

Genere 10⁴ muestras del mismo proceso. El total número de muestras satisface PoissonDistribution, con la media igual a la intensidad las veces del área de la región.

In[5]:=

samples = ppp[region, intensity, 10^4]; counts = Length /@ samples;

In[6]:=

htd = PearsonChiSquareTest[counts, PoissonDistribution[intensity RegionMeasure[region]], "HypothesisTestData"];

In[7]:=

htd["TestDataTable"]

Out[7]=

In[8]:=

htd["TestConclusion"]

Out[8]=

El número de puntos en cualquier subregión es también distribuido por Poisson. Aquí, esto se examina con un disco que yace dentro del polígono, y se cuenta el número de puntos en él.

In[9]:=

disk1 = Disk[{-107, 28}, 1.5]; Show[region, Graphics[{Red, disk1}]]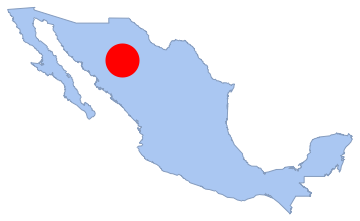

Out[9]=

In[10]:=

memberfun1 = RegionMember[disk1]; counts1 = Table[Total[Boole[memberfun1[pts]]], {pts, samples}];

Realice una prueba PearsonChiSquareTest en el número de cuentas dentro de una distribución de Poisson.

In[11]:=

htd = PearsonChiSquareTest[counts1, PoissonDistribution[intensity RegionMeasure[disk1]], "HypothesisTestData"];

In[12]:=

htd["TestDataTable"]

Out[12]=

In[13]:=

htd["TestConclusion"]

Out[13]=

El número de puntos en cualquier subregión disjunta es independiente. Aquí, se cuenta el número de puntos en los dos discos disjuntos, y se realiza una prueba de SpearmanRankTest.

In[14]:=

disk2 = Disk[{-100, 20}, 1.3]; Show[region, Graphics[{Red, disk1, Blue, disk2}]]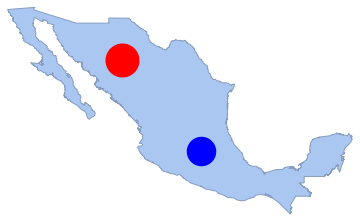

Out[14]=

In[15]:=

memberfun2 = RegionMember[disk2]; counts2 = Table[Total[Boole[memberfun2[pts]]], {pts, samples}];

In[16]:=

htd = SpearmanRankTest[counts1, counts2, "HypothesisTestData"];

In[17]:=

htd["TestDataTable"]

Out[17]=

In[18]:=

htd["TestConclusion"]

Out[18]=