Wolfram Language™

Salidas de registro de precios de acciones

Se supone que los precios de acciones modelados con el movimiento geométrico browniano (en el modelo clásico de Black–Scholes) son distribuidos normalmente en sus salidas de registro. Aquí esta premisa es examinada con los precios de acciones de cinco compañías: Google, Microsoft, Facebook, Apple e Intel.

Extraiga los precios de acciones en 2015 con FinancialData.

In[1]:=

symbols = {"GOOG", "MSFT", "FB", "AAPL", "INTC"}; prices = Table[ FinancialData[stock, {{2015, 1, 1}, {2015, 12, 31}}], {stock, symbols}];

Calcule las salidas de registro.

In[2]:=

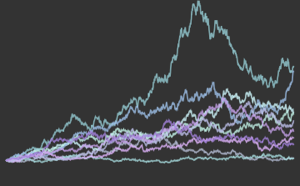
logreturn = Minus[Differences[Log[prices[[All, All, 2]]], {0, 1}]];

Filtre las salidas de registro con un ARCHProcess de orden 1.

In[3]:=

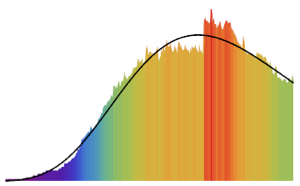
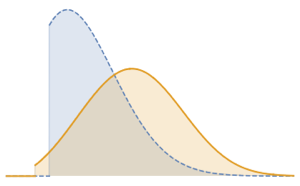
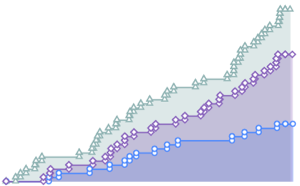
fdata = Table[ {\[Kappa]1, \[Alpha]1} = {\[Kappa], \[Alpha]} /. FindProcessParameters[lr, ARCHProcess[\[Kappa], {\[Alpha]}]]; MovingMap[Last[#]/Sqrt[\[Kappa]1 + \[Alpha]1 First[#]^2] &, lr, 2] , {lr, logreturn}]; fdata = Transpose[fdata];

Compare los datos filtrados de cada acción con la distribución normal con QuantilePlot. Para todas las cinco compañías, las colas se desvían de lo normal.

In[4]:=

MapThread[ QuantilePlot[#1, PlotLabel -> #2, PlotTheme -> "Detailed"] &, {Transpose[fdata], symbols}]

Out[4]=

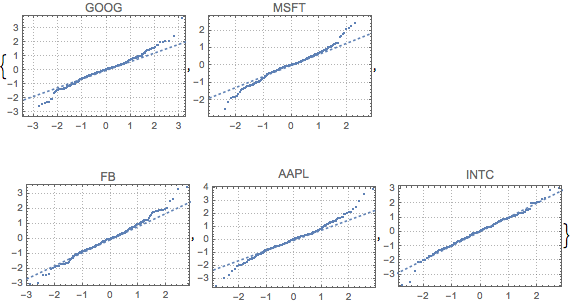
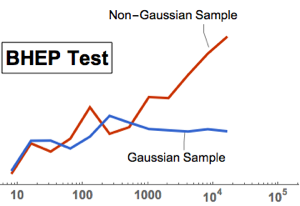
Realice una prueba multivariable de normalidad con BaringhausHenzeTest (BHEP). La hipótesis de normalidad es claramente rechazada.

In[5]:=

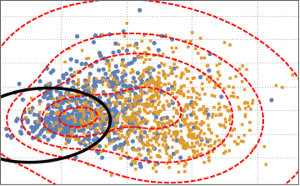
htd = BaringhausHenzeTest[fdata, "HypothesisTestData"];

In[6]:=

htd["TestDataTable"]

Out[6]=

In[7]:=

htd["ShortTestConclusion"]

Out[7]=

Ajuste los datos filtrados con MultinormalDistribution y MultivariateTDistribution.

In[8]:=

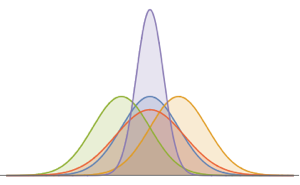
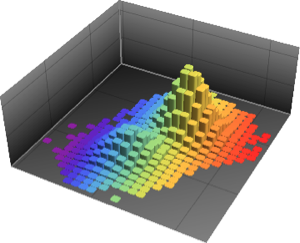
multiN = EstimatedDistribution[fdata, MultinormalDistribution[Array[x, 5], Array[s, {5, 5}]]]

Out[8]=

In[9]:=

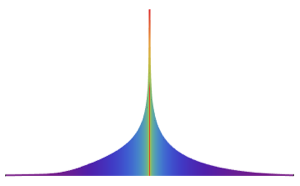
multiT = EstimatedDistribution[fdata, MultivariateTDistribution[Array[x, 5], Array[s, {5, 5}], nu]]

Out[9]=

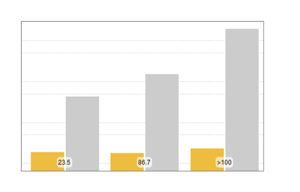
Calcule el AIC de dos distribuciones. El modelo de MultivariateTDistribution tiene un valor más pequeño.

In[10]:=

aic[k_, dist_, data_] := 2 k - 2 LogLikelihood[dist, data]

In[11]:=

aic[5 + 15, multiN, fdata]

Out[11]=

In[12]:=

aic[5 + 15 + 1, multiT, fdata]

Out[12]=