무게 구하기
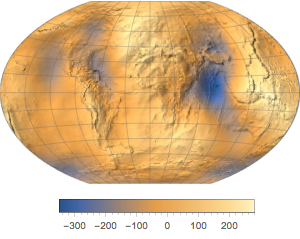
중력장에 있는 개체의 무게는 그 질량과 그 개체가 있는 지점에서의 중력장의 값을 곱한 값입니다. 지상에서는 중력장은 일정하지 않으므로 개체의 무게는 장소에 따라 다릅니다. 이 예에서는 고도와 위도에 따라 중력장의 크기가 어떻게 변하는지 알아봅니다.
GeogravityModelData는 지정된 지점에서 지구 중력장의 몇가지 특성을 계산합니다.
In[1]:=
GeogravityModelData[GeoPosition[{0, 0}]]Out[1]=

이것은 GeoElevationData가 제공하는 지리적 고도를 사용합니다.
In[2]:=
GeoElevationData[GeoPosition[{0, 0}]]Out[2]=
다른 영향을 무시하면 중력장은 유사한 위도의 위치에서 일반적으로 작아지고 고도가 높은 곳에서 커집니다.
In[3]:=
GeoPosition[Entity["City", {"Quito", "Pichincha", "Ecuador"}]]Out[3]=
In[4]:=
GeoPosition[Entity["City", {"Quito", "Pichincha", "Ecuador"}]];
{GeoElevationData[%, UnitSystem -> "Metric"],
GeogravityModelData[%, "Magnitude"]}Out[4]=
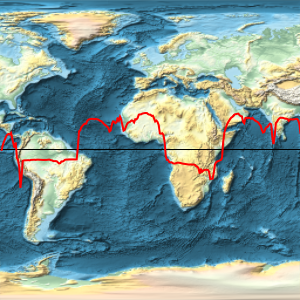
적도 등거리 지점에서 중력 필드의 값을 계산합니다.
In[5]:=

equatorialgravity =
GeogravityModelData[{GeoPosition[{0, -180}], GeoPosition[{5, 180}]},
"Magnitude"][[1]]Out[5]=

In[6]:=
ListPlot[equatorialgravity, Joined -> True]Out[6]=
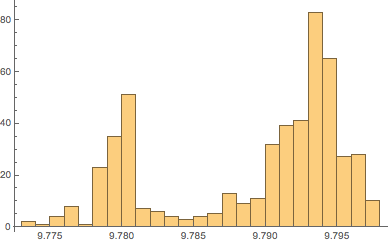
아래의 히스토그램은 육지 부분과 해저에 대응하는 큰 정점 두 개가 있습니다.
In[7]:=
Histogram[equatorialgravity, 20]Out[7]=
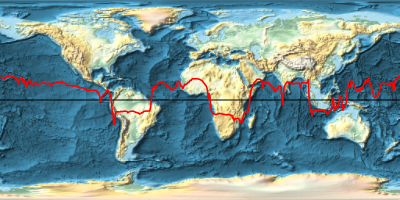
지구 기복도에 중력장의 크기를 겹쳐 놓습니다.
In[8]:=

equatorialgravityplot =
ListPlot[equatorialgravity, Axes -> False, Joined -> True,
AspectRatio -> 1/8, PlotRangePadding -> None, ImagePadding -> None,
ImageSize -> 400, PlotStyle -> Red];In[9]:=
worldmap =
GeoGraphics[GeoPath["Equator"], GeoRange -> "World",
ImageSize -> 400, GeoBackground -> "ReliefMap"];In[10]:=
Overlay[{worldmap, equatorialgravityplot}, Alignment -> Center]Out[10]=
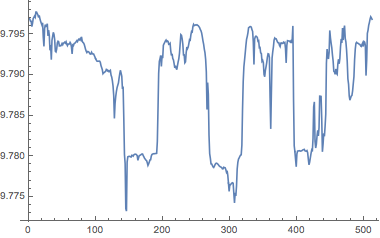
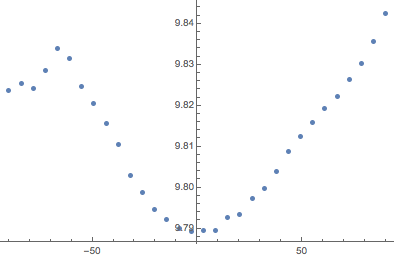
위도에 대한 변화를 나타내기 위해, 경도의 중력장의 크기를 평균하고 위도에 반하여 결과를 표현합니다.
In[11]:=

gravity =
Mean /@ GeogravityModelData[{GeoPosition[{-90, -180}],
GeoPosition[{90, 180}]}, "Magnitude"];고도가 더해짐으로 인해 남극은 저위도의 명백한 영향을 보여줍니다.
In[12]:=
ListPlot[gravity, DataRange -> {-90, 90}]Out[12]=
In[13]:=
MinMax[gravity]Out[13]=
따라서 지정된 개체의 무게 측정 위치에 따라 그 무게의 0.5% 정도가 달라질 수 있습니다.
In[14]:=
MinMax[gravity];
1 - First[%]/Last[%]