Ondes dans le Grand Lac Salé

À l'aide d'ImageMesh, vous pouvez convertir des segments d'image en objets BoundaryMeshRegion. Ces maillages vous permettent d'utiliser des fonctions dans d'autres aires, telles que les méthodes d'éléments finis (MEF).

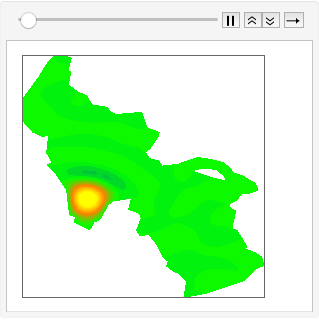
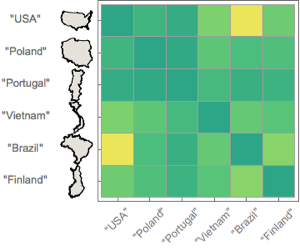
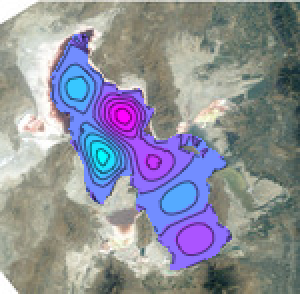
Pour illustrer cette connexion MEF, déterminez les principaux modes d'ondes de surface sur le Grand Lac Salé dans l'Utah.

In[1]:=

img = EntityValue[Entity["Lake", "GreatSaltLake::yw8cf"], "Image"]

Out[1]=

Régularisez l'image avec un filtre à décalage moyen.

In[2]:=

img2 = MeanShiftFilter[img, 3, 0.1]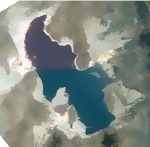

Out[2]=

Obtenez une segmentation par la croissance des régions.

In[3]:=

mask = RegionBinarize[img2, \!\(\* GraphicsBox[ TagBox[RasterBox[CompressedData[" 1:eJzt1jEKwkAQQNFdK0uv4C1sLW0VD6AYxSZCFMRzCJ7XiF3SzFb7lf8ggUCK D8MmM99f1sdJSuk67W/r3X3ZdbvHZtY/bNvr+dQ2h1V7a05Nt9h/Xnv21ytJ kiRJkiRJkn5H7tVuGLMqzqo4q+KsiuNW8bKsimNWfbNwXVbF5Yzuqp0xZFUB dBaui5kF/T5AsxJ1jNAsq0qgs3BlOSPDMrMLmvUBDcNnsbqov2x4FrWrdscA NIu6SjCzoEOEZlGniF5Ta0eMmVXCqjjmCJlV5KzaDWNWxXGreFnMKvAIazeM MUfIXEmtKsCs8hSWsCrOqjhmlSRJkiRJkvS/3tRrD1M= "], {{0, 147}, {150, 0}}, {0, 1}, ColorFunction->GrayLevel], BoxForm`ImageTag["Bit", ColorSpace -> Automatic, Interleaving -> None], Selectable->False], DefaultBaseStyle->"ImageGraphics", ImageSizeRaw->{150, 147}, PlotRange->{{0, 150}, {0, 147}}]\), 1/5]

Out[3]=

Récupérez un objet BoundaryMeshRegion de la surface du lac.

In[4]:=

\[ScriptCapitalR] = ImageMesh[mask]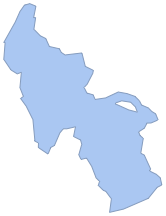

Out[4]=

Créez un maillage de la surface du lac.

In[5]:=

\[CapitalOmega] = TriangulateMesh[\[ScriptCapitalR], MaxCellMeasure -> 8]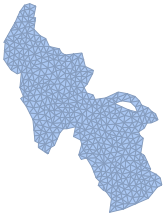

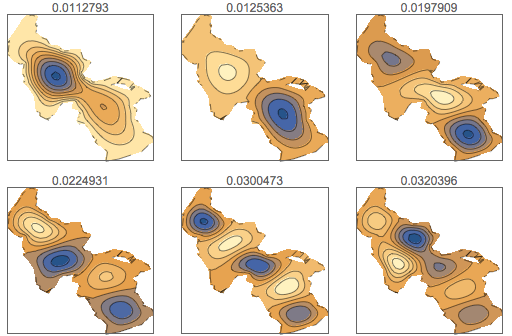
Out[5]=

Résolvez l'équation d'onde de la surface du lac en déterminant d'abord les fonctions propres du Laplacien à l'intérieur de la région du lac.

In[6]:=

\[ScriptCapitalL] = -\!\( \*SubsuperscriptBox[\(\[Del]\), \({x, y}\), \(2\)]\(\[CurlyPhi][x, y]\)\);

Utilisez une condition aux limite.

In[7]:=

\[ScriptCapitalB] = DirichletCondition[\[CurlyPhi][x, y] == 0, True];

Générez une base orthonormée de fonctions propres Φ avec valeurs propres Λ.

In[8]:=

{\[CapitalLambda], \[CapitalPhi]} = NDEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, \[CurlyPhi][x, y], {x, y} \[Element] \[CapitalOmega], 64];

Affichez les six premiers modes d'oscillation.

In[9]:=

GraphicsGrid[ Partition[ Table[ContourPlot[\[CapitalPhi][[ k]], {x, y} \[Element] \[CapitalOmega], PlotRange -> All, PlotLabel -> \[CapitalLambda][[k]], PlotTheme -> "Minimal"], {k, 6}], 3 ], ImageSize -> 512 ]

Out[9]=

L'évolution temporelle des modes d'oscillation en décomposition est donnée par ce qui suit.

In[10]:=

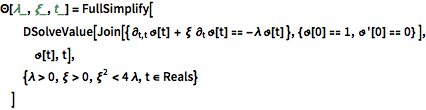
\[CapitalTheta][\[Lambda]_, \[Xi]_, t_] = FullSimplify[ DSolveValue[Join[{ \!\( \*SubscriptBox[\(\[PartialD]\), \(t, t\)]\(\(TraditionalForm\`\[CurlyTheta]\)[ t]\)\) + \[Xi] \!\( \*SubscriptBox[\(\[PartialD]\), \(t\)]\(\(TraditionalForm\`\ \[CurlyTheta]\)[ t]\)\) == -\[Lambda] \!\(TraditionalForm\`\[CurlyTheta]\)[ t] }, {\!\(TraditionalForm\`\[CurlyTheta]\)[0] == 1, \[CurlyTheta]'[0] == 0} ], \!\(TraditionalForm\`\[CurlyTheta]\)[t], t], {\[Lambda] > 0, \[Xi] > 0, \[Xi]^2 < 4 \[Lambda], t \[Element] Reals} ]

Out[10]=

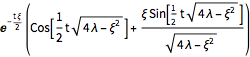
En développant une perturbation initiale en fonctions propres et en les laissant évoluer dans le temps, on obtient une simulation de la propagation des ondes à travers le lac.

In[11]:=

n = 64; weights = Take[GaussianMatrix[{{n}, n/2}], -n - 1]; weights -= Last[weights]; weights = Most[weights]; weights *= 1/First[weights]; wave[t_] = (\[CapitalTheta][\[CapitalLambda], 0.005, t] weights (\[CapitalPhi] /. {x -> 50, y -> 60} )) . \[CapitalPhi]; waveColors = (Blend[{{-0.01, Purple}, {-0.005, Blue}, {0., Green}, {0.005, Orange}, {0.01, Yellow}}, #] &); anim = Table[ ContourPlot[ wave[t], {x, y} \[Element] \[CapitalOmega], PlotRange -> {-0.01, 0.012}, Contours -> Range[-0.01, 0.012, 0.0005], PlotTheme -> "Minimal", ColorFunctionScaling -> False, ContourStyle -> None, ColorFunction -> waveColors ], {t, 0, 255, 1} ]; ListAnimate[anim]

Jouer l'animation

Arrêter l'annimation