Generate Oscillations in a Circular Membrane: New in Wolfram Language 11

‹›

Generate Oscillations in a Circular Membrane

Model the oscillations of a circular membrane of radius 1 using the wave equation in 2D.

In[1]:=

eqn = r D[u[r, t], {t, 2}] == D[r D[u[r, t], r], r];

Specify that the boundary of the membrane remain fixed.

In[2]:=

bc = u[1, t] == 0;

Initial condition for the problem.

In[3]:=

ic = {u[r, 0] == 0, Derivative[0, 1][u][r, 0] == 1};

Obtain a solution in terms of Bessel functions, using DSolve.

In[4]:=

(dsol = DSolve[{eqn, bc, ic}, u[r, t], {r, t}]) // TraditionalForm

Out[4]//TraditionalForm=

Extract a finite number of terms from the Inactive sum.

In[5]:=

h[r_, t_] = 
  u[r, t] /. dsol[[1]] /. {\[Infinity] -> 3} // Activate // N;

The lowest mode has a period of approximately 2.612.

In[6]:=

N[(2 \[Pi])/BesselJZero[0, 1]]

Out[6]=

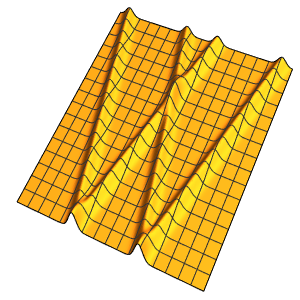
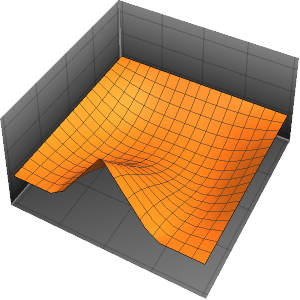
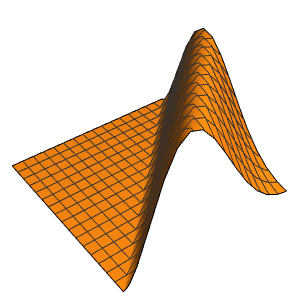
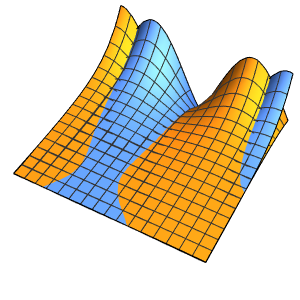
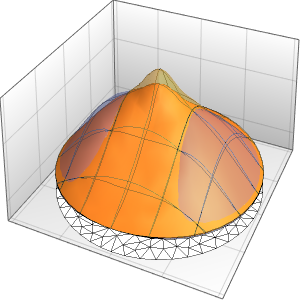
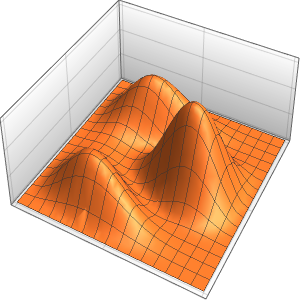
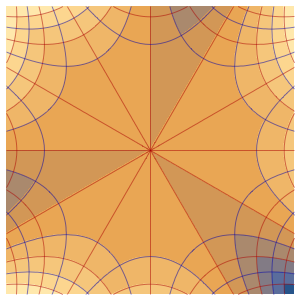
Visualize the oscillations of the membrane over four periods.

In[7]:=

ListAnimate[
 Table[Plot3D[
   Evaluate[h[r, t] /. {r -> Sqrt[x^2 + y^2]}], {x, y} \[Element] 
    Disk[], PlotRange -> {-1, 1}, Ticks -> None, Mesh -> True, 
   MeshStyle -> {Red, Blue}, PlotStyle -> Yellow, Boxed -> False, 
   Axes -> False, ImageSize -> Medium, AspectRatio -> 1, 
   Background -> Lighter[Orange, 0.85]], {t, 0, 10.45, 0.05}]]