Observación de una partícula cuántica en una caja: Nuevo en Wolfram Language 11

Observación de una partícula cuántica en una caja

Una partícula cuántica libre de moverse dentro de un rectángulo de dos dimensiones con lados xMax y 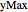se describe como una ecuación de Schrödinger dependiente del tiempo, junto con condiciones de límite que obligan a la función de onda a cero en el límite.

In[1]:=

eqn = I D[\[Psi][x, y, t], t] == -\[HBar]^2/(2 m)
     Laplacian[\[Psi][x, y, t], {x, y}];

In[2]:=

bcs = {\[Psi][0, y, t] == 0, \[Psi][xMax, y, t] == 
    0, \[Psi][x, yMax, t] == 0, \[Psi][x, 0, t] == 0};

Esta ecuación tiene una solución general que es una suma formal infinita de los llamados estados propios.

In[3]:=

DSolveValue[{eqn, bcs}, \[Psi][x, y, t], {x, y, t}]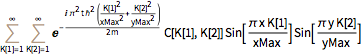

Out[3]=

Defina una condición inicial igual a un estado propio unificado.

In[4]:=

initEigen = \[Psi][x, y, 0] == 
   2 /Sqrt[xMax yMax] Sin[(\[Pi] x)/xMax] Sin[(\[Pi] y)/yMax];

En este caso, la solución es simplemente una múltiple (de la unidad de módulo) dependiente del tiempo de la condición inicial.

In[5]:=

DSolveValue[{eqn, bcs, initEigen}, \[Psi][x, y, t], {x, y, t}]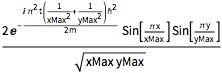

Out[5]=

Defina una condición inicial que es la suma de estados propios. Debido a que las condiciones iniciales no constituyen un estado inicial, la densidad de probabilidad para la ubicación de la partícula será dependiente del tiempo.

In[6]:=

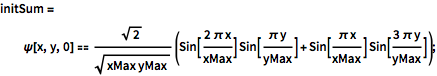
initSum = \[Psi][x, y, 0] == 
   Sqrt[2]/Sqrt[
    xMax yMax] (Sin[(2 \[Pi] x)/xMax] Sin[(\[Pi] y)/yMax] + 
      Sin[(\[Pi] x)/xMax] Sin[(3 \[Pi] y)/yMax]);

Resuelva con una nueva condición inicial.

In[7]:=

sol = DSolveValue[{eqn, bcs, initSum}, \[Psi][x, y, t], {x, y, t}]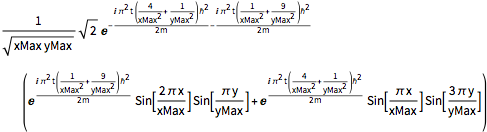

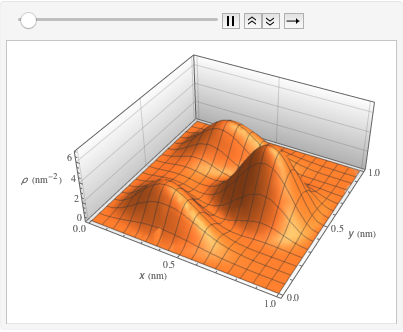
Out[7]=

Calcule la densidad de probabilidad, agregando valores de la constante reducida de Planck, masa de electrón y una caja de tamaño atómico, utilizando unidades de la masa del electrón, nanómetros y femtosegundos.

In[8]:=

\[HBar] = 
 QuantityMagnitude[Quantity[1., "ReducedPlanckConstant"], 
  "ElectronMass" * ("Nanometers")^2/"Femtoseconds"]

Out[8]=

In[9]:=

\[Rho][x_, y_, t_] = 
 FullSimplify[ComplexExpand[Conjugate[sol] sol]] /. {m -> 1, 
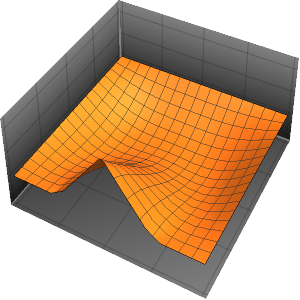
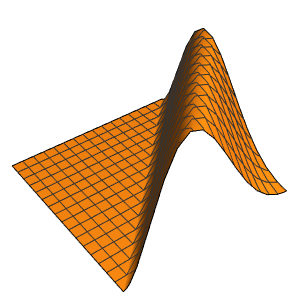
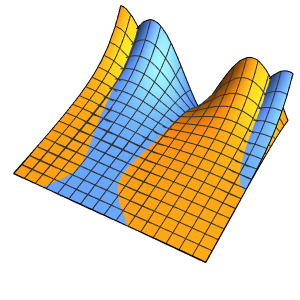
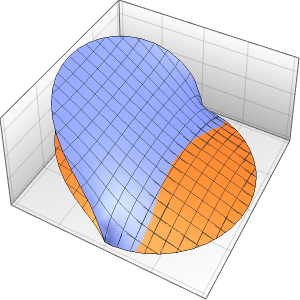
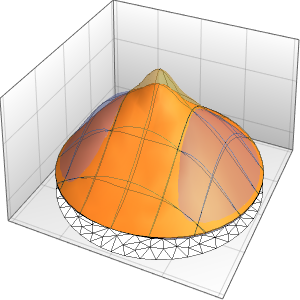
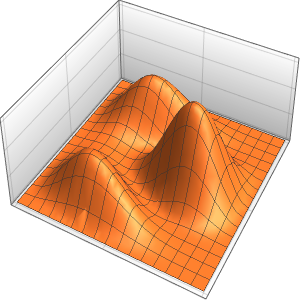
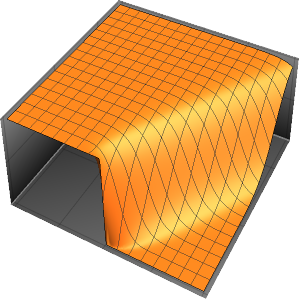
   xMax -> 1, yMax -> 1}

Out[9]=

Visualice la probabilidad dentro de la caja con el tiempo.

In[10]:=

ListAnimate[
 Table[Plot3D[\[Rho][x , y , t], {x, 0, 1}, {y, 0, 1}, 
   PlotTheme -> {"Scientific", "SolidGrid"}, AxesLabel -> {"\!\(\*
StyleBox[\"x\", \"SO\"]\) (nm)", " \!\(\*
StyleBox[\"y\", \"SO\"]\) (nm)", "\!\(\*
StyleBox[\"\[Rho]\", \"SO\"]\) (\!\(\*SuperscriptBox[\(nm\), \
\(-2\)]\))"}, ImageSize -> Medium, PlotRange -> {0, 7}], {t, 0, 
   19, .5}]]