Modelo del flujo de calor en una barra con aislamiento
Modele el flujo de calor en una barra de longitud 1 que ha sido aislada en ambos extremos.
In[1]:=
heqn = D[u[x, t], t] == D[u[x, t], {x, 2}];Especifique que no hay calor que fluya a través de los extremos de la barra.
In[2]:=
bc = {Derivative[1, 0][u][0, t] == 0, Derivative[1, 0][u][1, t] == 0};Especifique una condición inicial.
In[3]:=
ic = u[x, 0] == 20 + 80 x;Resuelva la ecuación de calor sujeta a estas condiciones.
In[4]:=
sol = DSolve[{heqn, bc, ic}, u[x, t], {x, t}]Out[4]=
Extraiga unos cuantos términos de la suma de Inactive.
In[5]:=
approxsol =
u[x, t] /. sol[[1]] /. {Infinity -> 4} // Activate // ExpandOut[5]=
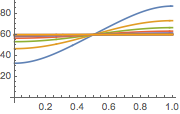
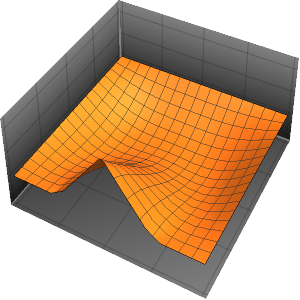
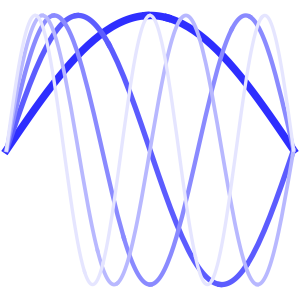
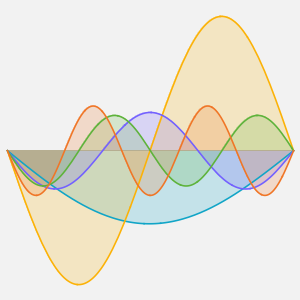
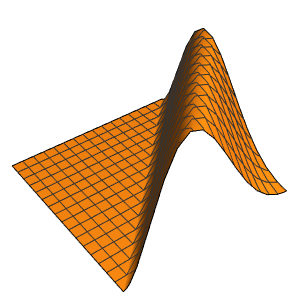
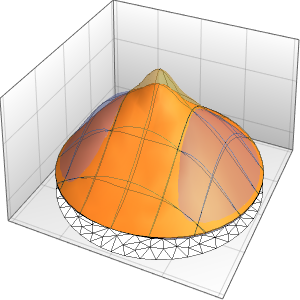
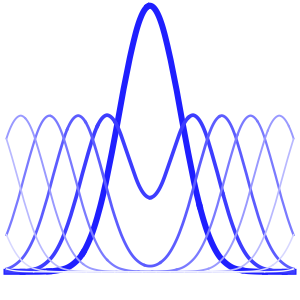
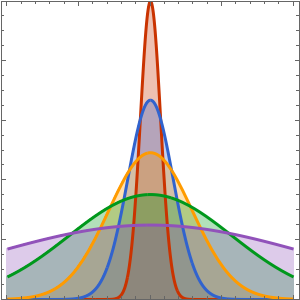
Visualice la evolución de la temperatura en un valor estable de 60°.
In[6]:=
Plot[Table[approxsol, {t, 0.02, 0.9, 0.07}] // Evaluate, {x, 0, 1},
AxesOrigin -> {0, 0}, PlotRange -> All]Out[6]=