Construcción de una función analítica compleja
Construya una función analítica compleja, empezando por los valores de sus partes reales e imaginarias en el eje 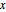 .
.
Las partes reales e imaginarias u y v satisfacen las ecuaciones de Cauchy–Riemann.
In[1]:=
creqns = {D[u[x, y], x] == D[v[x, y], y],
D[v[x, y], x] == -D[u[x, y], y]};Establezca los valores de u y v en el eje 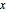 .
.
In[2]:=
xvals = {u[x, 0] == x^3, v[x, 0] == 0};Resuelva las ecuaciones de Cauchy–Riemann.
In[3]:=
sol = DSolve[{creqns, xvals}, {u, v}, {x, y}]Out[3]=
Verifique que las soluciones sean armónicas.
In[4]:=
Laplacian[{u[x, y], v[x, y]} /. sol[[1]], {x, y}]Out[4]=
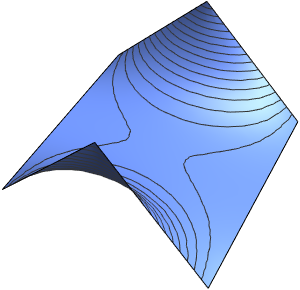
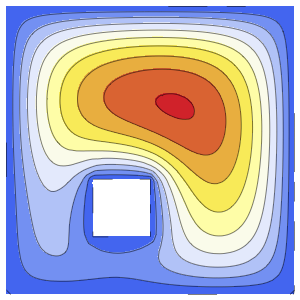
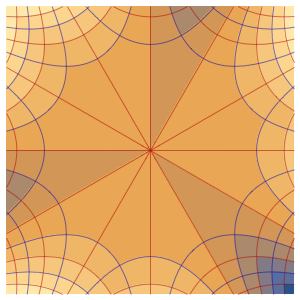
Visualice las líneas de flujo y equipotenciales generadas por la solución.
In[5]:=
ContourPlot[{u[x, y], v[x, y]} /. sol[[1]], {x, -5, 5}, {y, -5, 5},
ContourStyle -> {Red, Blue}]Out[5]=
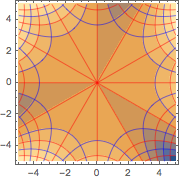
Construya una función analítica desde la solución.
In[6]:=
f[x_, y_] = u[x, y] + I v[x, y] /. sol[[1]]Out[6]=
Esto representa la función 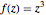 .
.
In[7]:=
(f[x, y] // Factor) /. {x + I y -> z}Out[7]=