Resuelva un problema de valor inicial para una ecuación de calor
Especifique la ecuación de calor.
In[1]:=
heqn = D[u[x, t], t] == D[u[x, t], {x, 2}];Establezca una condición inicial para la ecuación.
In[2]:=
ic = u[x, 0] == E^(-x^2);Resuelva el problema de valor inicial.
In[3]:=
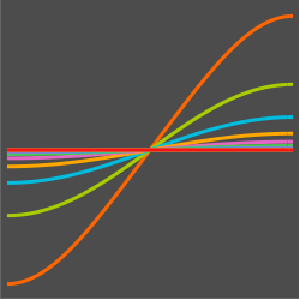
sol = DSolveValue[{heqn, ic }, u[x, t], {x, t}]Out[3]=
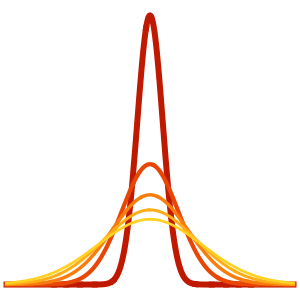
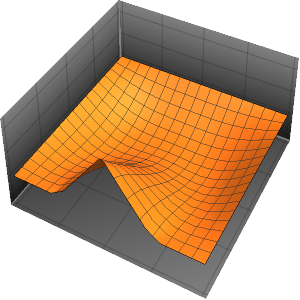
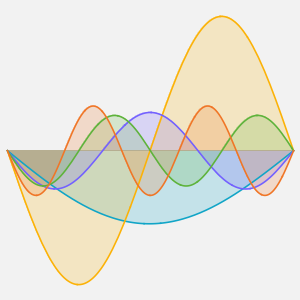
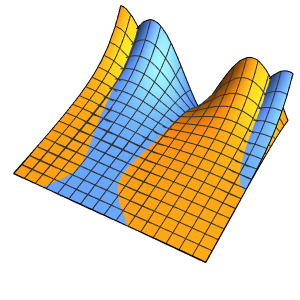
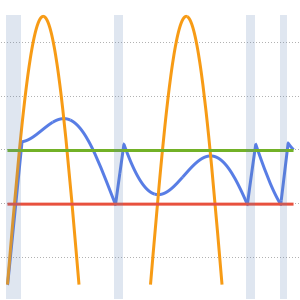
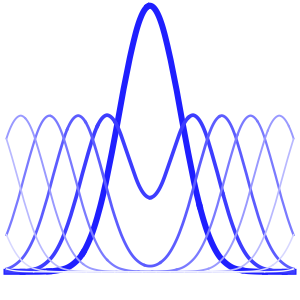
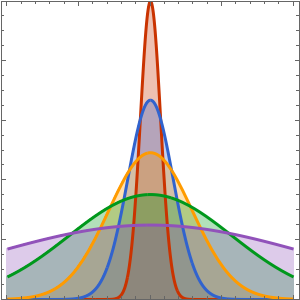
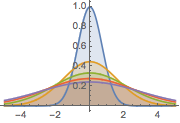
Visualice la difusión de calor con el paso del tiempo.
In[4]:=
Plot[Evaluate[Table[sol, {t, 0, 4}]], {x, -5, 5}, PlotRange -> All,
Filling -> Axis]Out[4]=
Problema de valor inicial para la ecuación de calor con datos iniciales definidos por partes.
In[5]:=
ic = u[x, 0] == UnitBox[x];In[6]:=
sol = DSolveValue[{heqn, ic }, u[x, t], {x, t}]Out[6]=
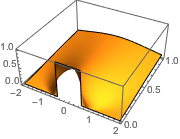
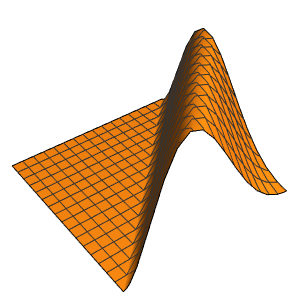
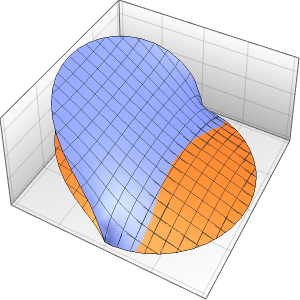
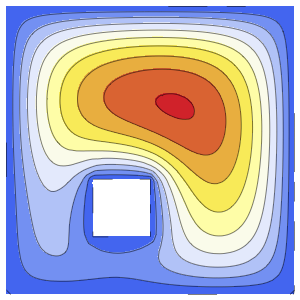
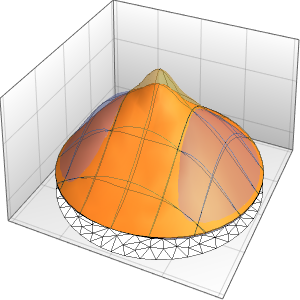
Las discontinuidades en los datos iniciales son suavizadas al instante.
In[7]:=
Plot3D[sol, {x, -2, 2}, {t, 0, 1}, PlotRange -> All,
PlotPoints -> 250, Mesh -> None]Out[7]=