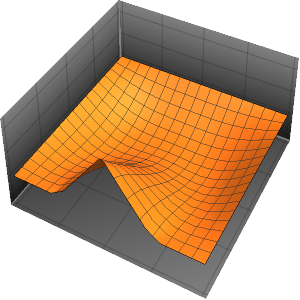
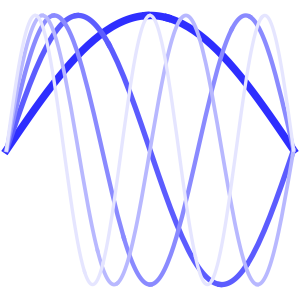
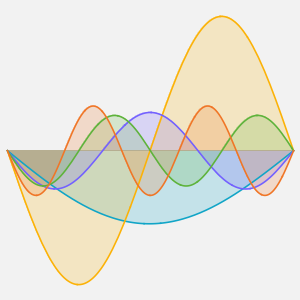
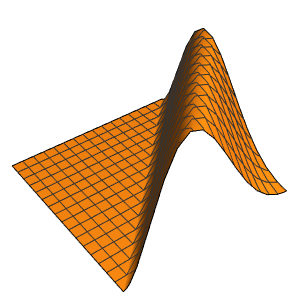
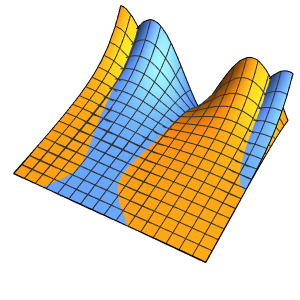
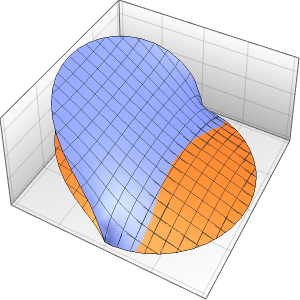
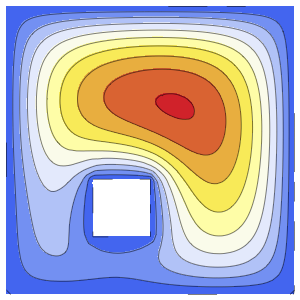
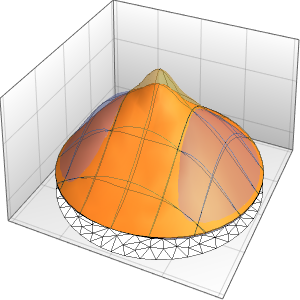
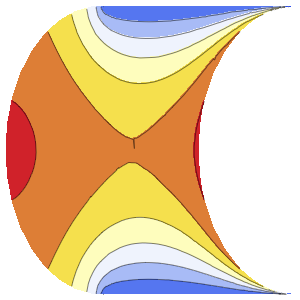
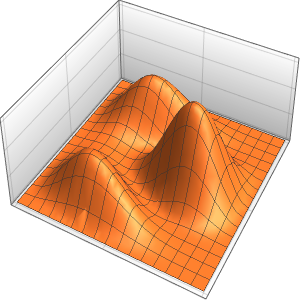
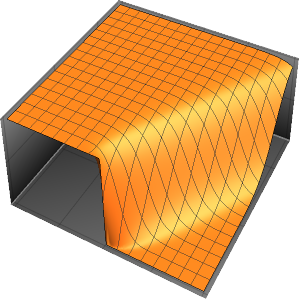
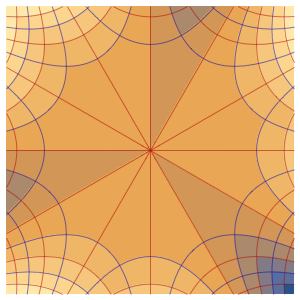
Solución de una ecuación de onda con condiciones de límite absorbentes
Resuelva una ecuación de onda en 1D con condiciones de límite absorbentes.
Especifique una ecuación de onda con condiciones de límite absorbentes. Note que el valor de Neumann es por primera vez derivado de 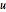 .
.
In[1]:=
eqn = D[u[t, x], {t, 2}] ==
D[u[t, x], {x, 2}] +
NeumannValue[-Derivative[1, 0][u][t, x], x == 0 || x == 1];Especifique las condiciones iniciales para la ecuación de onda.
In[2]:=
u0[x_] := Evaluate[D[0.125 Erf[(x - 0.5)/0.125], x]];
ic = {u[0, x] == u0[x], Derivative[1, 0][u][0, x] == 0};Resuelva la ecuación usando el método de elemento finito.
In[3]:=

ufun = NDSolveValue[{eqn, ic}, u, {t, 0, 1}, {x, 0, 1},
Method -> {"MethodOfLines",
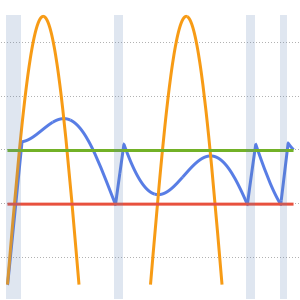
"SpatialDiscretization" -> {"FiniteElement"}}];Visualice la ecuación de onda con condiciones de límite absorbentes.
In[4]:=
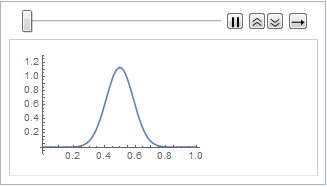
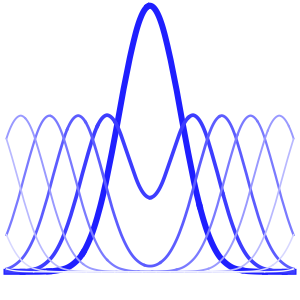
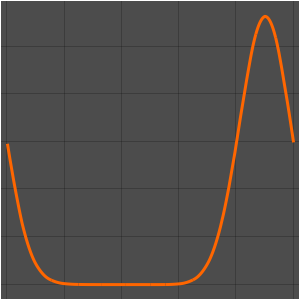
list = Table[
Plot[ufun[t, x], {x, 0, 1}, PlotRange -> {-0.1, 1.3}], {t, 0, 1,
0.1}];
ListAnimate[list]