Наблюдение за квантовой частицей в двухмерном прямоугольнике : Новое в системе Wolfram Language 11

Наблюдение за квантовой частицей в двухмерном прямоугольнике

Квантовая частица, свободно передвигающаяся в двухмерном прямоугольнике со сторонами xMax и yMax, описана двухмерным динамичным уравнением Шрёдингера, а также граничными условиями, которые заставляют волновую функцию стремится к нулю на границе.

In[1]:=

eqn = I D[\[Psi][x, y, t], t] == -\[HBar]^2/(2 m)
     Laplacian[\[Psi][x, y, t], {x, y}];

In[2]:=

bcs = {\[Psi][0, y, t] == 0, \[Psi][xMax, y, t] == 
    0, \[Psi][x, yMax, t] == 0, \[Psi][x, 0, t] == 0};

Уравнение имеет общее решение, которое является формальной бесконечной суммой так называемых собственных состояний.

In[3]:=

DSolveValue[{eqn, bcs}, \[Psi][x, y, t], {x, y, t}]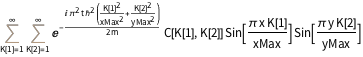

Out[3]=

Определить начальное условие, которое равно цельному собственному состоянию.

In[4]:=

initEigen = \[Psi][x, y, 0] == 
   2 /Sqrt[xMax yMax] Sin[(\[Pi] x)/xMax] Sin[(\[Pi] y)/yMax];

В данном случае, решением является простое динамичное кратное число (модулей единиц измерения) начального условия.

In[5]:=

DSolveValue[{eqn, bcs, initEigen}, \[Psi][x, y, t], {x, y, t}]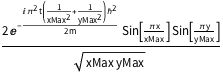

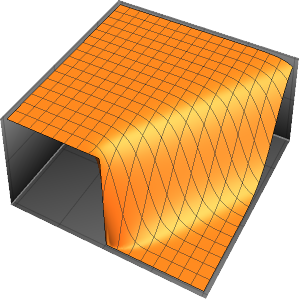
Out[5]=

Определить начальное условие, которое является суммой собственных состояний. Поскольку начальные условия не являются собственным состоянием, вероятная плотность положения частицы будет зависеть от времени.

In[6]:=

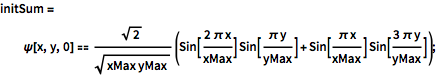
initSum = \[Psi][x, y, 0] == 
   Sqrt[2]/Sqrt[
    xMax yMax] (Sin[(2 \[Pi] x)/xMax] Sin[(\[Pi] y)/yMax] + 
      Sin[(\[Pi] x)/xMax] Sin[(3 \[Pi] y)/yMax]);

Решить с новым начальным условием.

In[7]:=

sol = DSolveValue[{eqn, bcs, initSum}, \[Psi][x, y, t], {x, y, t}]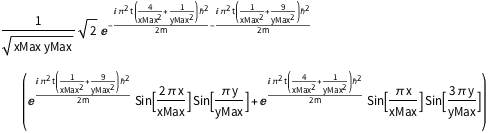

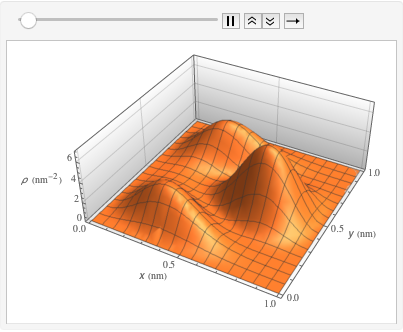
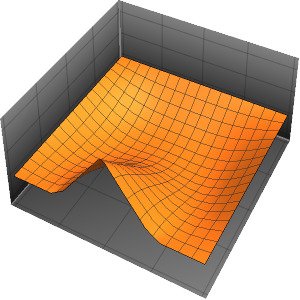
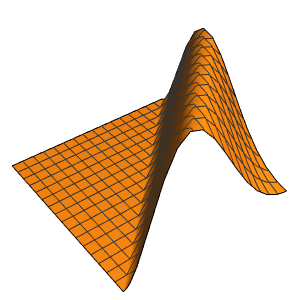
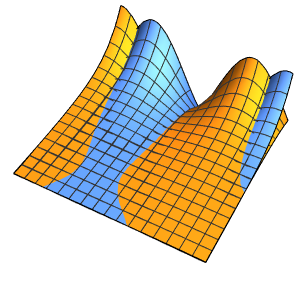
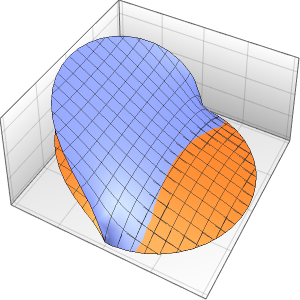
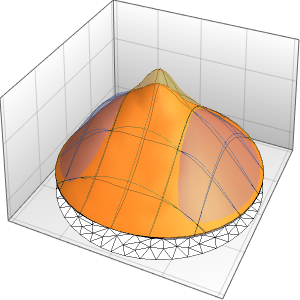
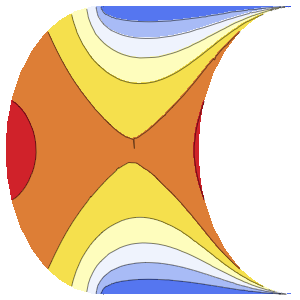
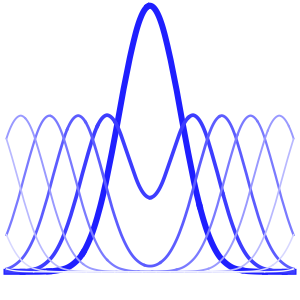
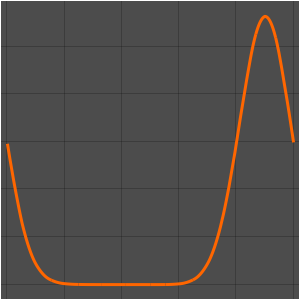
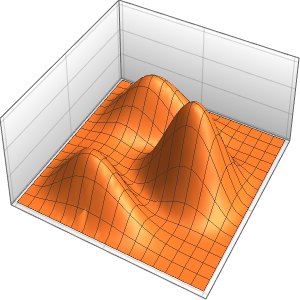
Out[7]=

Рассчитать плотность вероятности, вводя значения уменьшенной константы Планка, массы электрона и двухмерного прямоугольникa атомных масштабов с использованием единиц измерения массы электрона, таких как нанометры и фемтосекунды.

In[8]:=

\[HBar] = 
 QuantityMagnitude[Quantity[1., "ReducedPlanckConstant"], 
  "ElectronMass" * ("Nanometers")^2/"Femtoseconds"]

Out[8]=

In[9]:=

\[Rho][x_, y_, t_] = 
 FullSimplify[ComplexExpand[Conjugate[sol] sol]] /. {m -> 1, 
   xMax -> 1, yMax -> 1}

Out[9]=

Визуализировать плотность вероятности внутри двухмерного прямоугольникa с течением времени.

In[10]:=

ListAnimate[
 Table[Plot3D[\[Rho][x , y , t], {x, 0, 1}, {y, 0, 1}, 
   PlotTheme -> {"Scientific", "SolidGrid"}, AxesLabel -> {"\!\(\*
StyleBox[\"x\", \"SO\"]\) (nm)", " \!\(\*
StyleBox[\"y\", \"SO\"]\) (nm)", "\!\(\*
StyleBox[\"\[Rho]\", \"SO\"]\) (\!\(\*SuperscriptBox[\(nm\), \
\(-2\)]\))"}, ImageSize -> Medium, PlotRange -> {0, 7}], {t, 0, 
   19, .5}]]