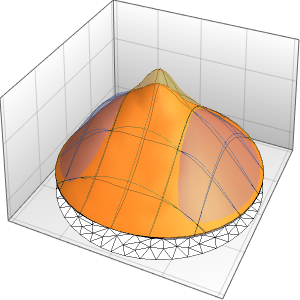
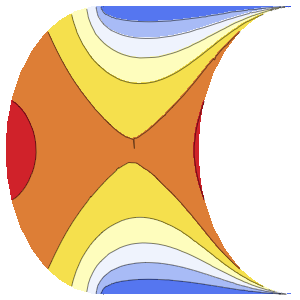
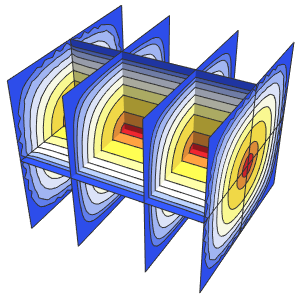
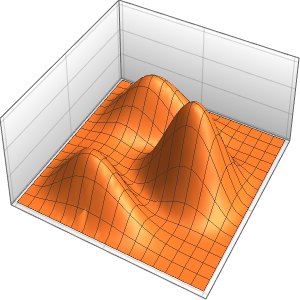
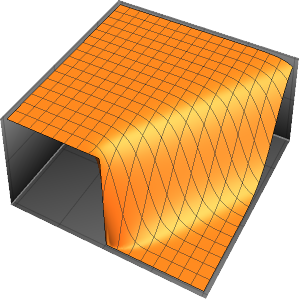
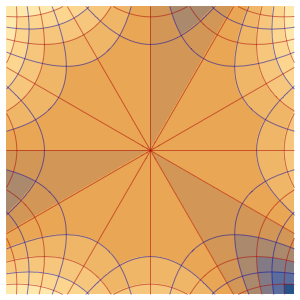
Решение волнового уравнения с периодическими граничными условиями
Решить волновое уравнение с периодическими граничными условиями в одномерной среде.
Задать волновое уравнение с поглощающими граничными условиями. Значение Неймана является производной от 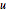 .
.
In[1]:=
eqn = D[u[t, x], {t, 2}] ==
D[u[t, x], {x, 2}] +
NeumannValue[-Derivative[1, 0][u][t, x], x == 0 || x == 1];Задать начальные условия для волнового уравнения.
In[2]:=

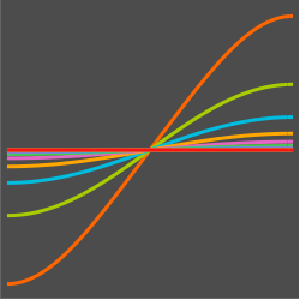
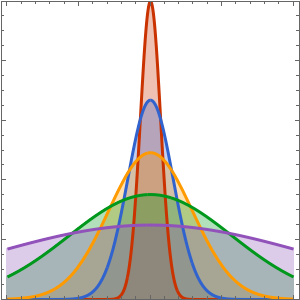
f[x_] = D[0.125 Erf[(x - 0.5)/0.125], x];
vInit[x_] = -D[f[x], x];
ic = {u[0, x] == f[x], Derivative[1, 0][u][0, x] == vInit[x]};Задать периодическое граничное условие таким образом, чтобы решение правой границы распространялось и на левую границу.
In[3]:=
bc = PeriodicBoundaryCondition[u[t, x], x == 0,
TranslationTransform[{1}]];Решить уравнение, используя метод конечных элементов.
In[4]:=
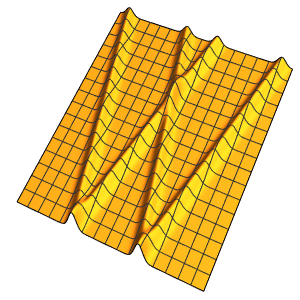
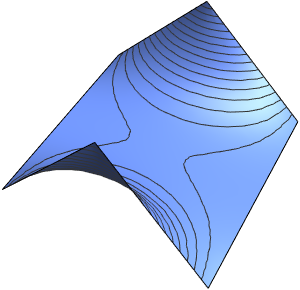
ufun = NDSolveValue[{eqn, ic, bc}, u, {t, 0, 2}, {x, 0, 1},
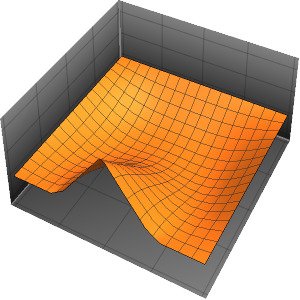
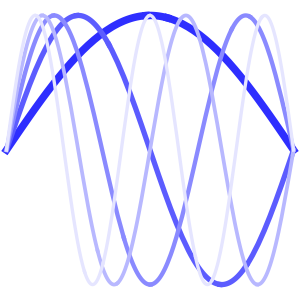
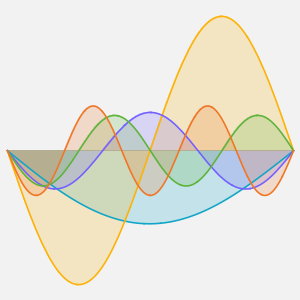
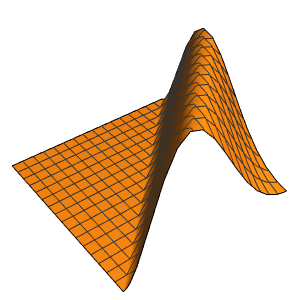
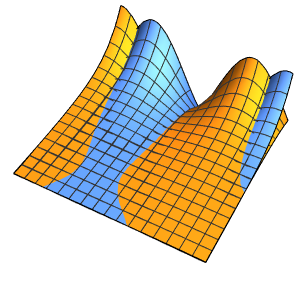
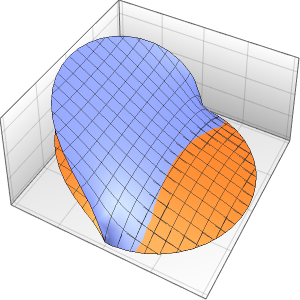
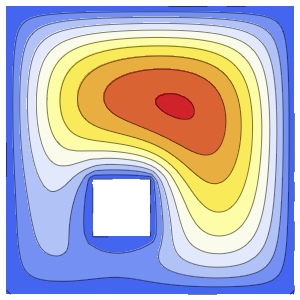
Method -> {"MethodOfLines"}];Визуализировать периодическую волновую функцию.
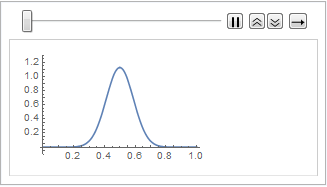
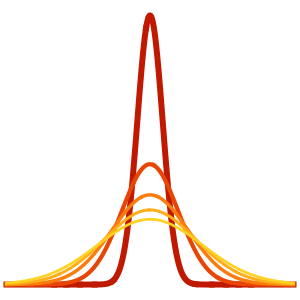
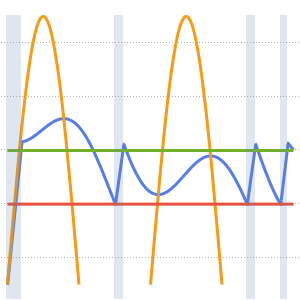
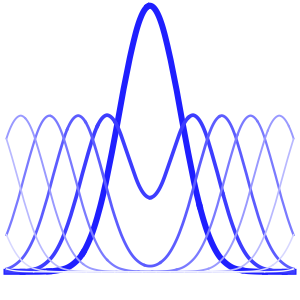
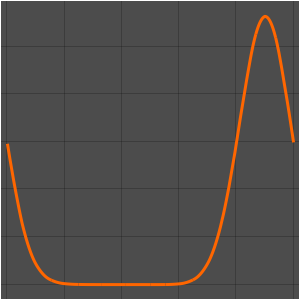
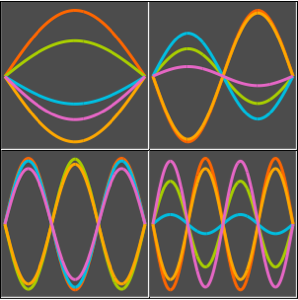
In[5]:=
plots = Table[
Plot[ufun[t, x], {x, 0, 1}, PlotRange -> {-0.1, 1.3}], {t, 0,
2, .1}];
ListAnimate[plots]