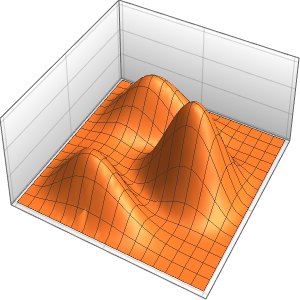
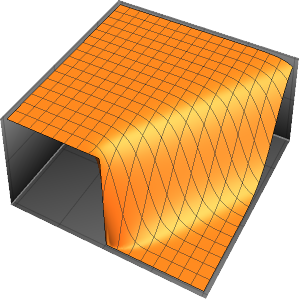
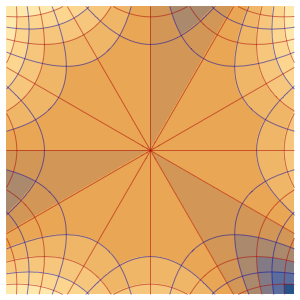
Моделирование потока тепла в изолированном брусе
Смоделировать поток тепла в брусе длиной =1, изолированном с обеих сторон.
In[1]:=
heqn = D[u[x, t], t] == D[u[x, t], {x, 2}];Указать, что тепло не протекает через концы бруса.
In[2]:=
bc = {Derivative[1, 0][u][0, t] == 0, Derivative[1, 0][u][1, t] == 0};Задать начальное условие.
In[3]:=
ic = u[x, 0] == 20 + 80 x;Решить тепловое уравнение, подпадающее под действие данных условий.
In[4]:=
sol = DSolve[{heqn, bc, ic}, u[x, t], {x, t}]Out[4]=
Извлечь несколько свободных элементов из неактивной (Inactive) суммы.
In[5]:=
approxsol =
u[x, t] /. sol[[1]] /. {Infinity -> 4} // Activate // ExpandOut[5]=
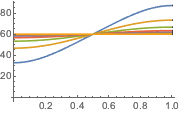
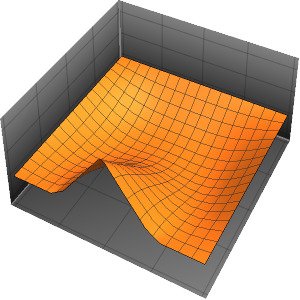
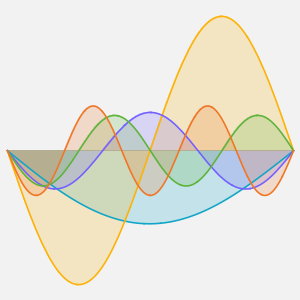
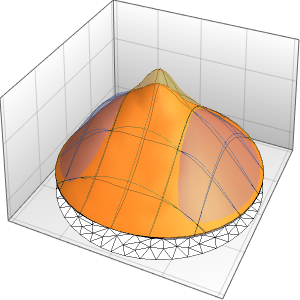
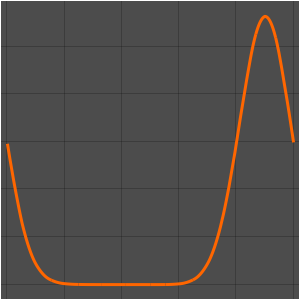
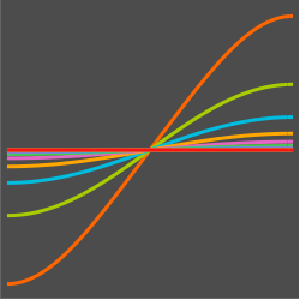
Визуализировать процесс изменения температуры до устойчивого значения 60°.
In[6]:=
Plot[Table[approxsol, {t, 0.02, 0.9, 0.07}] // Evaluate, {x, 0, 1},
AxesOrigin -> {0, 0}, PlotRange -> All]Out[6]=