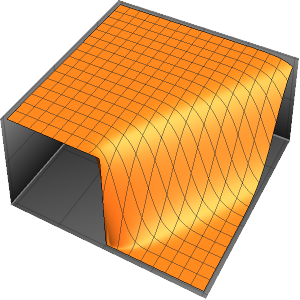
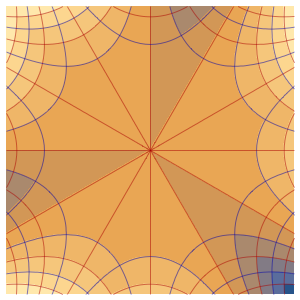
Resolva uma equação de onda com condições de contorno absorventes
Resolva uma equação de onda em 1D com condições de contorno absorventes.
Especifique uma equação de onda com condições de contorno absorventes. Note que o valor de Neumann é pela primeira vez derivado de 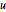 .
.
In[1]:=
eqn = D[u[t, x], {t, 2}] ==
D[u[t, x], {x, 2}] +
NeumannValue[-Derivative[1, 0][u][t, x], x == 0 || x == 1];Especifique as condições iniciais para a equação de onda.
In[2]:=
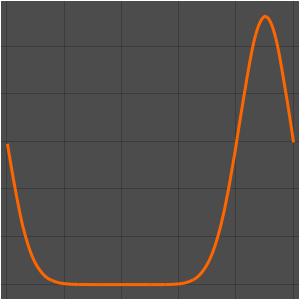
u0[x_] := Evaluate[D[0.125 Erf[(x - 0.5)/0.125], x]];
ic = {u[0, x] == u0[x], Derivative[1, 0][u][0, x] == 0};Resolva a equação utilizando o método de elemento finito.
In[3]:=

ufun = NDSolveValue[{eqn, ic}, u, {t, 0, 1}, {x, 0, 1},
Method -> {"MethodOfLines",
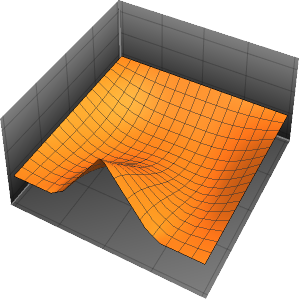
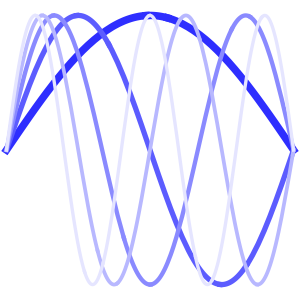
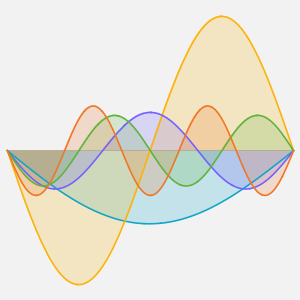
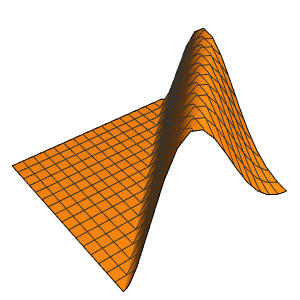
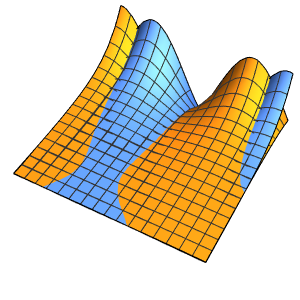
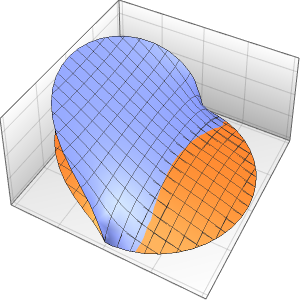
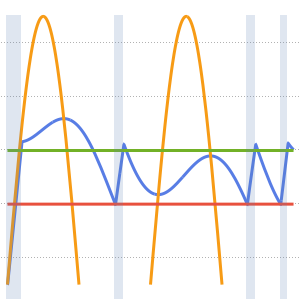
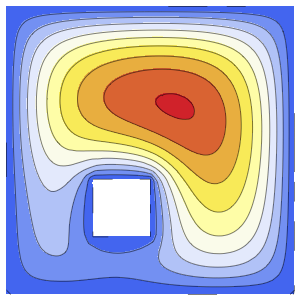
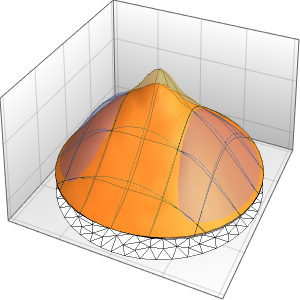
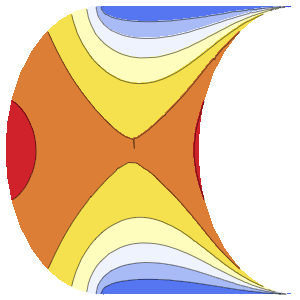
"SpatialDiscretization" -> {"FiniteElement"}}];Visualize a equação com condições de contorno absorventes.
In[4]:=
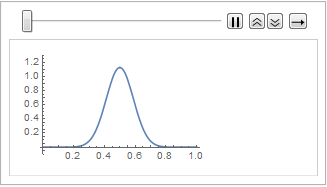
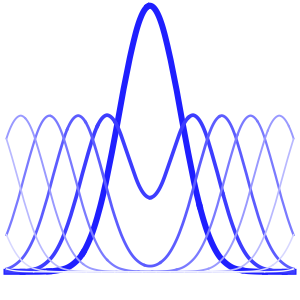
list = Table[
Plot[ufun[t, x], {x, 0, 1}, PlotRange -> {-0.1, 1.3}], {t, 0, 1,
0.1}];
ListAnimate[list]