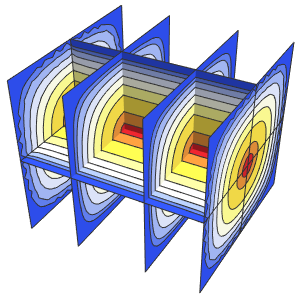
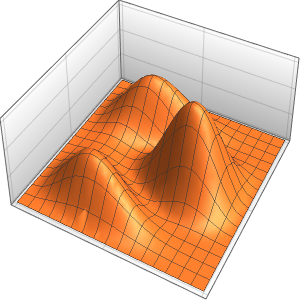
Calcule sensibilidades de equações diferenciais parciais sobre regiões
Calcule a dependência paramétrica de uma equação de onda 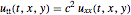 ,
, 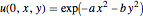 .
.
Especifique a equação de onda 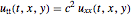 .
.
In[1]:=
eqn = D[u[t, x, y], t, t] == c^2 Laplacian[u[t, x, y], {x, y}];Especifique as condições iniciais 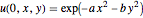 .
.
In[2]:=
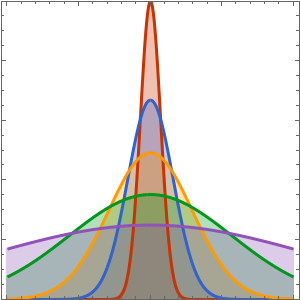
ics = {u[0, x, y] == Exp[-((a x)^2 + (b x)^2)],
Derivative[1, 0, 0][u][0, x, y] == 0};Especifique uma condição de contorno de Dirichlet fixa.
In[3]:=
bcs = DirichletCondition[u[t, x, y] == 0, True];Configure a função paramétrica.
In[4]:=
pfun = ParametricNDSolveValue[{eqn, ics, bcs},
u, {t, 0, 5}, {x, y} \[Element] Disk[], {a, b, c}];Encontre as sensibilidades 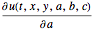 ,
,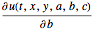 , e
, e 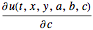 para os parâmetros
para os parâmetros 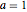 ,
, 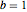 , and
, and 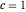 .
.
In[5]:=

ifda = D[pfun[a, 1, 1], a] /. {a -> 1};
ifda = D[pfun[1, b, 1], b] /. {b -> 1};
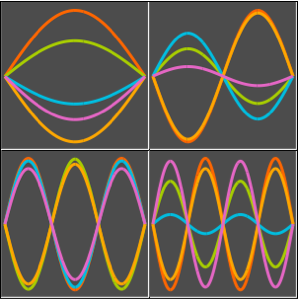
ifdc = D[pfun[1, 1, c], c] /. {c -> 1};Visualize as bandas de sensibilidade correspondentes fazendo um gráfico da função paramétrica para 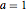 ,
, 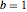 , e
, e 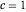 at
at 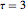 e sobrepondo a solução com
e sobrepondo a solução com 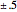 da sensibilidade.
da sensibilidade.
In[6]:=
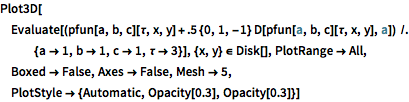
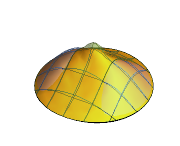
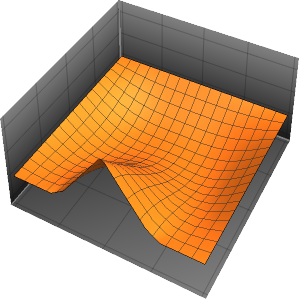
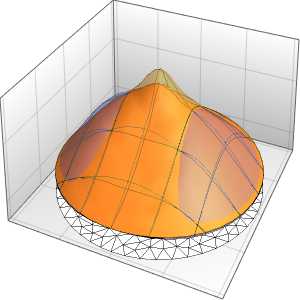
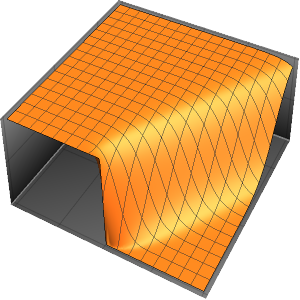
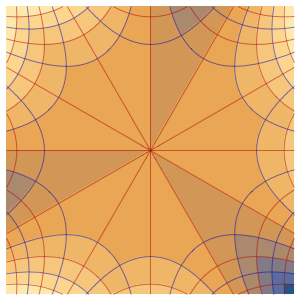
Plot3D[Evaluate[(pfun[a, b, c][\[Tau], x,
y] + .5 {0, 1, -1} D[pfun[a, b, c][\[Tau], x, y], a]) /. {a ->
1, b -> 1, c -> 1, \[Tau] -> 3}], {x, y} \[Element] Disk[],
PlotRange -> All, Boxed -> False, Axes -> False, Mesh -> 5,
PlotStyle -> {Automatic, Opacity[0.3], Opacity[0.3]}]Out[6]=