Construa uma função analítica complexa

Construa uma função analítica complexa, começando pelos seus valores de suas partes reais e imaginárias no eixo on the .

As partes reais e imaginárias u e v satisfazem as equações de Cauchy–Riemann.

In[1]:=

creqns = {D[u[x, y], x] == D[v[x, y], y], D[v[x, y], x] == -D[u[x, y], y]};

Estabeleça os valores de u e v no eixo .

In[2]:=

xvals = {u[x, 0] == x^3, v[x, 0] == 0};

Resolva as equações de Cauchy–Riemann.

In[3]:=

sol = DSolve[{creqns, xvals}, {u, v}, {x, y}]

Out[3]=

Verifique se as soluções são funções harmônicas.

In[4]:=

Laplacian[{u[x, y], v[x, y]} /. sol[[1]], {x, y}]

Out[4]=

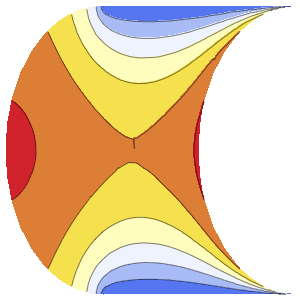
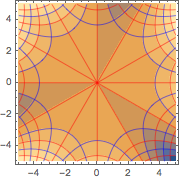
Visualize as linhas de fluxo e equipotenciais geradas pela solução.

In[5]:=

ContourPlot[{u[x, y], v[x, y]} /. sol[[1]], {x, -5, 5}, {y, -5, 5}, ContourStyle -> {Red, Blue}]

Out[5]=

Construa uma função analítica complexa da solução.

In[6]:=

f[x_, y_] = u[x, y] + I v[x, y] /. sol[[1]]

Out[6]=

Isto representa a função .

In[7]:=

(f[x, y] // Factor) /. {x + I y -> z}

Out[7]=