Zufallsvektoren mit verschiedenen Einheiten

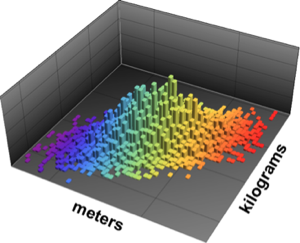
Bestimmen Sie eine multivariate Höhen-Gewichtsverteilung mit einer angenommenen Korrelation von 0,65.

In[1]:=

hw\[ScriptCapitalD] = BinormalDistribution[{Quantity[1.8, "Meters"], Quantity[85, "Kilograms"]}, {Quantity[0.15, "Meters"], Quantity[9, "Kilograms"]}, 0.65]

Out[1]=

Berechnen Sie die Wahrscheinlichkeit, dass eine Person größer als 1,75 m ist, bei einem gegebenen Körpergewicht von über 72 kg.

In[2]:=

NProbability[ h > Quantity[1.75, "m"] \[Conditioned] w > Quantity[72, "kg"], {h, w} \[Distributed] hw\[ScriptCapitalD]]

Out[2]=

Berechnen Sie die Verteilung des Body Mass Index (BMI) der angenommenen Population.

In[3]:=

bmi\[ScriptCapitalD] = TransformedDistribution[ w/h^2, {h, w} \[Distributed] hw\[ScriptCapitalD]]

Out[3]=

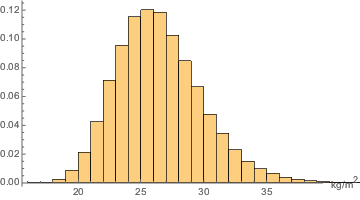
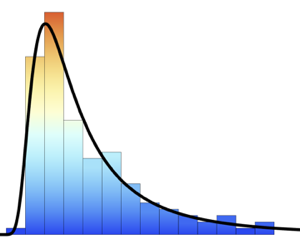
Schätzen Sie die Verteilung des BMI mithilfe eines Histogramms.

In[4]:=

sample = RandomVariate[bmi\[ScriptCapitalD], 10^5]; Histogram[sample, Automatic, "PDF", AxesLabel -> Automatic]

Out[4]=