Gestutzte Verteilung mit Mengen
Der Durchschnitt einer amerikanischen Cranberry folgt einer Normalverteilung mit Mittelwert 16 mm und Standardabweichung 1,6 mm. Eine Beere muss einen Durchmesser von mindesten 15 mm haben, um ganz verkauft zu werden, sonst wird sie zu Cranberrysauce weiterverarbeitet. Ermitteln Sie die Größenverteilung der Früchte, die ganz verkauft werden.
In[1]:=
cran\[ScriptCapitalD] =
NormalDistribution[Quantity[16, "Millimeters"],
Quantity[1.6, "Millimeters"]];
\[ScriptCapitalD] =
TruncatedDistribution[{Quantity[15, "Millimeters"], \[Infinity]},
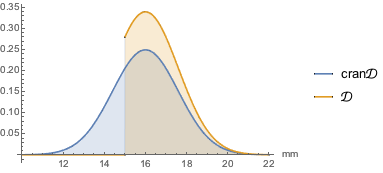
cran\[ScriptCapitalD]];Vergleichen Sie die Wahrscheinlichkeitsdichtefunktionen.
In[2]:=

Plot[{PDF[cran\[ScriptCapitalD], Quantity[x, "Milimeters"]],
PDF[\[ScriptCapitalD], Quantity[x, "Milimeters"]]}, {x, 10, 22},
PlotLegends -> {"cran\[ScriptCapitalD]", "\[ScriptCapitalD]"},
Filling -> Axis, AxesLabel -> {"mm"}]Out[2]=
Ermitteln Sie auf Basis der Annahme, dass ein 500g-Körbchen Cranberries ein Volumen von rund 30 in3 hat, die durchschnittliche Unter- und Obergrenze für die Anzahl der Cranberries in einem solchen Körbchen.
In[3]:=

lowerbound =
Floor[NExpectation[
Divide[Quantity[30, "Inches"^3],
Volume[Cuboid[{0, 0, 0}, {x, x, x}]]],
x \[Distributed] \[ScriptCapitalD]]]Out[3]=
In[4]:=

upperbound =
Ceiling[NExpectation[
Divide[Quantity[30, "Inches"^3], Volume[Ball[{0, 0, 0}, x/2]]],
x \[Distributed] \[ScriptCapitalD]]]Out[4]=