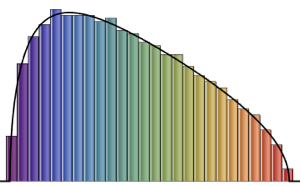
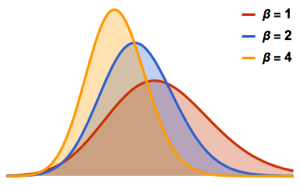
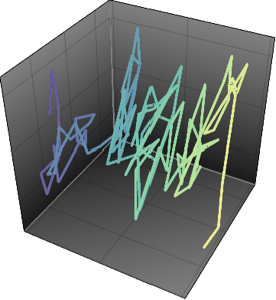
Einen Vektor-AR-Prozess simulieren
Simulieren Sie mit MatrixNormalDistribution einen Vektor-autoregressiven Prozess.
In[1]:=
sigR = Covariance[ARProcess[{a}, 1][Range[0, 100]]];
sigC = {{s11, s12}, {s12, s22}};In[2]:=
rules = {a -> 1/2, s11 -> 1, s12 -> 1/2, s22 -> 3};In[3]:=
\[ScriptCapitalD] = MatrixNormalDistribution[sigR, sigC] /. rules;Simulieren Sie eine zufällige Stichprobe der Matrixverteilung.
In[4]:=
vals = RandomVariate[\[ScriptCapitalD], 10^4];Erzeugen Sie TemporalData aus den Stichprobenwerten.
In[5]:=
td = TemporalData[vals, {0, Length[sigR] - 1, 1},
ValueDimensions -> 2]Out[5]=
Schätzen Sie den diagonalen Vektor-autoregressiven Prozess.
In[6]:=
proc = ARProcess[{a IdentityMatrix[2]}, sigC];In[7]:=
sol = FindProcessParameters[td, proc]Out[7]=
Vergleichen Sie mit den ursprünglichen Werten.
In[8]:=
sol[[All, 2]] - rules[[All, 2]]Out[8]=