Wolfram Language™

Zirkulare Ensembles (COE, CUE, ...)

Ein zirkulares Ensemble ist die Gesamtheit unitärer Matritzen mit Verteilungen, die unter unterschiedlichen unitären Transformationen unveränderlich bleiben. Typische Anwendungsgebiete sind statistische Mechanik, Zahlentheorie, Kombinatorik und Atomphysik.

Matritzen des zirkular reellen Ensembles (CRE) sind orthogonal.»

In[1]:=

cre = RandomVariate[CircularRealMatrixDistribution[5]];

In[2]:=

OrthogonalMatrixQ[cre]

Out[2]=

Matritzen des zirkular unitären Ensembles (CUE) sind unitär.»

In[3]:=

cue = RandomVariate[CircularUnitaryMatrixDistribution[5]];

In[4]:=

UnitaryMatrixQ[cue]

Out[4]=

Matritzen des zirkular orthogonalen Ensemble (COE) sind symmetrisch und unitär.»

In[5]:=

coe = RandomVariate[CircularOrthogonalMatrixDistribution[5]];

In[6]:=

SymmetricMatrixQ[coe] && UnitaryMatrixQ[coe]

Out[6]=

Matritzen des zirkular symplektischen Ensemble (CSE) sind selbstdual unitär quaternionisch.»

In[7]:=

selfdualQuaternionicQ[m_] := With[{\[ScriptCapitalJ] = KroneckerProduct[{{0, -1}, {1, 0}}, IdentityMatrix[Length[m]/2]], mat = SetAccuracy[m, 10]}, Transpose[mat].\[ScriptCapitalJ] == \[ScriptCapitalJ].mat];

In[8]:=

cse = RandomVariate[CircularSymplecticMatrixDistribution[5]];

In[9]:=

UnitaryMatrixQ[cse] && selfdualQuaternionicQ[cse]

Out[9]=

Matritzen des zirkular quaternionischen Ensembles (CQE) sind symplektisch unitär.»

In[10]:=

symplecticMatrixQ[mat_] := With[{\[ScriptCapitalJ] = KroneckerProduct[{{0, -1}, {1, 0}}, IdentityMatrix[Length[mat]/2]] }, Conjugate[mat].\[ScriptCapitalJ] == \[ScriptCapitalJ].mat];

In[11]:=

cqe = RandomVariate[CircularQuaternionMatrixDistribution[5]];

In[12]:=

UnitaryMatrixQ[cqe] && symplecticMatrixQ[cqe]

Out[12]=

Eigenwerte von Matritzen des CUE, COE und CSE haben eine Einheitslänge und sind gleichphasig uniformverteilt.

In[13]:=

args = Flatten[ Arg[RandomVariate[ MatrixPropertyDistribution[Eigenvalues[x], x \[Distributed] #], 10^4]]] & /@ {CircularUnitaryMatrixDistribution[5], CircularOrthogonalMatrixDistribution[5], CircularSymplecticMatrixDistribution[5]}; Row[MapThread[ Histogram[#1, {-Pi, Pi, Pi/10}, Frame -> None, ChartLegends -> Placed[#2, Above]] &, {args, {Style["Unitary", 15], Style["Orthogonal", 15], Style["Symplectic", 15]}}]]

Out[13]=

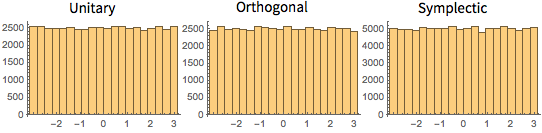
Visualisieren Sie die multivariate Verteilung der Phase der Eigenwerte eines zweidimensionalen CUE und vergleichen Sie diese mit der tatsächlichen Dichte.

In[14]:=

evs\[ScriptCapitalD] = MatrixPropertyDistribution[Arg[Eigenvalues[x]], x \[Distributed] CircularUnitaryMatrixDistribution[2]]; \[CurlyPhi]s = RandomSample /@ RandomVariate[evs\[ScriptCapitalD], 10^5];

In[14]:=

Show[ Histogram3D[\[CurlyPhi]s, {-Pi, Pi, 0.25}, PDF, PlotTheme -> "Scientific", ChartStyle -> "AvocadoColors"], Plot3D[1/(8 Pi^2) Abs[Exp[I \[Phi]1] - Exp[I \[Phi]2]]^2, {\[Phi]1, -Pi, Pi}, {\[Phi]2, -Pi, Pi}, PlotStyle -> None, MeshStyle -> Thick], ImageSize -> Medium]

Out[15]=

In[16]:=

Show[ Histogram3D[\[CurlyPhi]s, {-Pi, Pi, 0.25}, PDF, ChartStyle -> "AvocadoColors"], Plot3D[1/(8 Pi^2) Abs[Exp[I \[Phi]1] - Exp[I \[Phi]2]]^2, {\[Phi]1, -Pi, Pi}, {\[Phi]2, -Pi, Pi}, PlotStyle -> None, MeshStyle -> Thick, PlotTheme -> "Marketing"], ImageSize -> Medium, Axes -> False]