Längste aufsteigende Teilfolgen

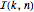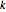Die Anzahl der Permutationen von Elementen, bei der die längste aufsteigende Teilfolge die maximale Länge hat, kann durch die Ermittlung des Durchschnitts über 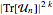berechnet werden, wobei 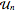Matritzen einer CircularUnitaryMatrixDistribution der Dimension sind.

In[1]:=

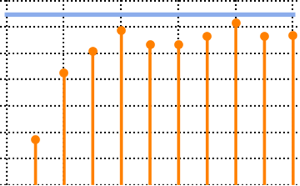
{k, n} = {6, 2};

Bestimmen Sie die Verteilung der Matrixeigenschaft und berechnen Sie den Mittelwert.

In[2]:=

\[ScriptCapitalD] = MatrixPropertyDistribution[Abs[Tr[\[ScriptCapitalU]]]^( 2 k), \[ScriptCapitalU] \[Distributed] CircularUnitaryMatrixDistribution[n]]; N[Mean[\[ScriptCapitalD]]]

Out[2]=

Vergleichen Sie mit der direkten Zählung.

In[3]:=

Count[Permutations[Range[k]], perm_ /; Length[LongestOrderedSequence[perm]] <= n]

Out[3]=

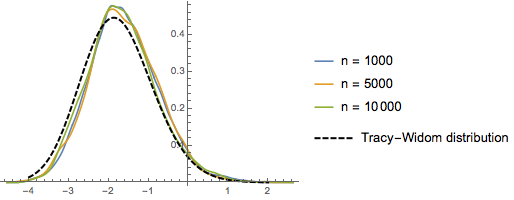
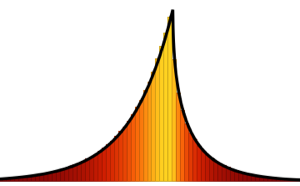
Bei 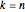konvergiert die Verteilung der skalierten Längen der längsten ansteigenden Teilfolge zufälliger Permutationen gegen die Tracy–Widom-Verteilung mit .

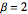In[4]:=

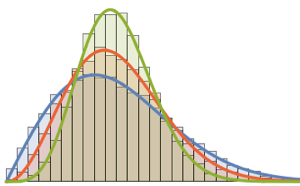
sample[n_] := 1/n^(1/6) (Table[ Length[LongestOrderedSequence[ RandomSample[Range[n]]]], {2000}] - 2.0 Sqrt[n]);

Vergleichen Sie das geglättete Histogramm der skalierten Längen mit der WDF der Tracy–Widom-Verteilung.

In[5]:=

dims = {1000, 5000, 10000}; Show[ SmoothHistogram[sample /@ dims, PlotLegends -> (Row[{"n = ", #}] & /@ dims)], Plot[PDF[TracyWidomDistribution[2], x], {x, -4, 2}, PlotStyle -> {Black, Dashed, Thick}, PlotLegends -> {"Tracy-Widom distribution"}]]

Out[5]=