Matrix-Normalverteilung und Matrix-T-Verteilung

Matrix-Normalverteilungen und Matrix-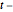Verteilungen sind matrixvariate Normalverteilungen und 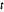-Verteilungen mit bestimmten Zeilen- und Spaltenmatritzen. Typische Einsatzgebiete sind die Zeitreihenanalyse, Zufallsprozesse und die multivariate Regression.

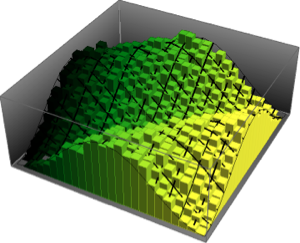
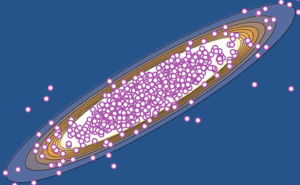
Gegeben seien die Skalematritzen Σ_row und Σ_col. Die Matrix-Normalverteilung hat eine Wahrscheinlichkeitsdichte, die proportional zu 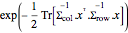ist. Nehmen Sie Stichproben aus einer Matrix-Normalverteilung.

In[1]:=

Subscript[\[CapitalSigma], row] = {{1, 0.9}, {0.9, 1}}; Subscript[\[CapitalSigma], col] = {{1, -0.9}, {-0.9, 1}};

In[2]:=

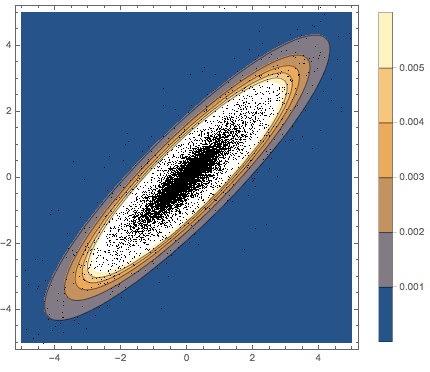
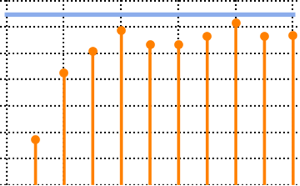
RandomVariate[ MatrixNormalDistribution[Subscript[\[CapitalSigma], row], Subscript[\[CapitalSigma], col]]]

Out[2]=

Visualisieren Sie die Zeilenvektoren in einem Streudiagramm und vergleichen Sie dieses mit der Dichtefunktion.

In[3]:=

sample = RandomVariate[ MatrixNormalDistribution[Subscript[\[CapitalSigma], row], Subscript[\[CapitalSigma], col]], 10^4]; firstrows = sample[[All, 1]];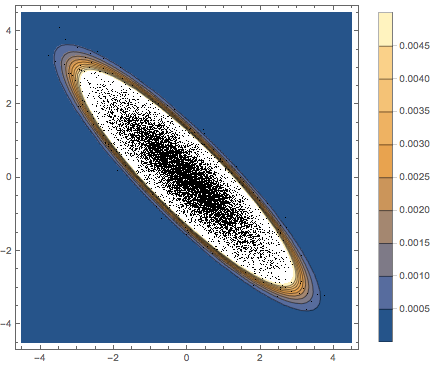

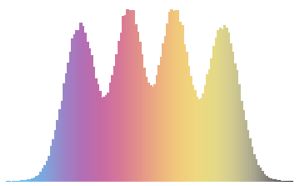
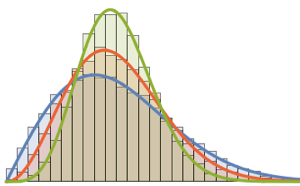
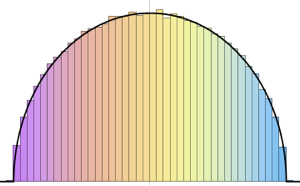
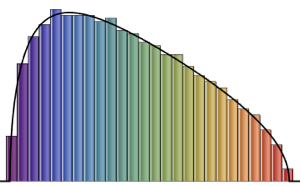
In[4]:=

Show[ContourPlot[ PDF[MultinormalDistribution[{0, 0}, Subscript[\[CapitalSigma], col] ], {x, y}], {x, -4.5, 4.5}, {y, -4.5, 4.5}, PlotPoints -> 30, PlotTheme -> "Detailed", ImageSize -> Medium], ListPlot[firstrows, ImageSize -> Medium, PlotTheme -> "Detailed", PlotStyle -> Black]]

Out[4]=

Visualisieren Sie die Spaltenvektoren in einem Histogramm und vergleichen Sie dieses mit einer Dichtefunktion.

In[5]:=

firstcols = sample[[All, All, 1]];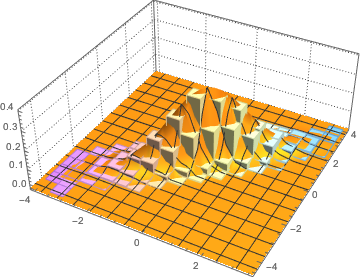

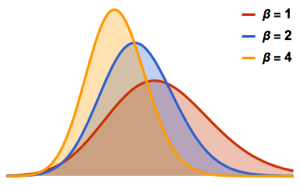
In[6]:=

Show[Histogram3D[firstcols, Automatic, "PDF", ImageSize -> Medium, PlotTheme -> "Detailed", ChartStyle -> "Pastel"], Plot3D[PDF[ MultinormalDistribution[{0, 0}, Subscript[\[CapitalSigma], row] ], {x, y}], {x, -5, 5}, {y, -5, 5}, PlotRange -> All, ImageSize -> Medium, PlotTheme -> "Detailed", PlotLegends -> None]]

Out[6]=

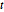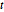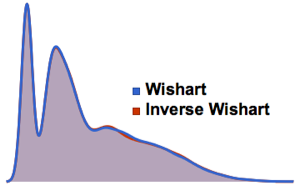
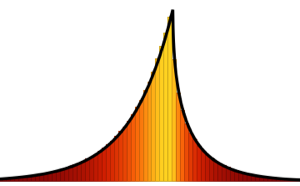
Ähnlich wie die Student--Verteilung und multivariate -Verteilungen ist die Matrix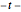Verteilung eine Mischung aus einer Matrix-Normalverteilung und einem inversen Wishart-verteilten Skalenparameter. Nehmen Sie Stichproben einer Matrix- 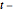Verteilung.

In[7]:=

RandomVariate[ MatrixTDistribution[Subscript[\[CapitalSigma], row], Subscript[\[CapitalSigma], col], 3]]

Out[7]=

Generieren Sie einen Satz von Matrix-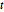-verteilten Matritzen.

In[8]:=

sample = RandomVariate[ MatrixTDistribution[Subscript[\[CapitalSigma], row], Subscript[\[CapitalSigma], col], 3], 10^4];

Niedrigdimensionale Projektionen von Matrix-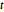-verteilten Zufallsvariablen sind Student 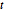- und multivariate 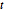-verteilt. Projizieren Sie die Stichprobe in zweidimensionale Vektoren und überprüfen Sie die Anpassungsgüte (goodness of fit).

In[9]:=

v = {1, 2}; vecs = sample.v;

In[10]:=

DistributionFitTest[vecs, MultivariateTDistribution[ Subscript[\[CapitalSigma], row] (v.Subscript[\[CapitalSigma], col].v)/3, 3]]

Out[10]=

Visualisieren Sie die projizierten Daten auf einem Streudiagramm und vergleichen Sie dieses mit der Dichtefunktion.

In[11]:=

Show[ContourPlot[ PDF[MultivariateTDistribution[ Subscript[\[CapitalSigma], row] (v.Subscript[\[CapitalSigma], col].v)/3, 3], {x, y}], {x, -5, 5}, {y, -5, 5}, PlotPoints -> 30, PlotTheme -> "Detailed", ImageSize -> Medium], ListPlot[vecs, ImageSize -> Medium, PlotTheme -> "Detailed", PlotStyle -> Black]]

Out[11]=