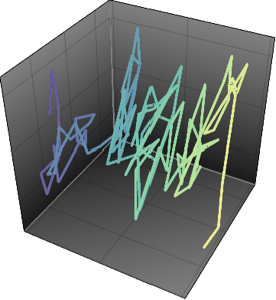
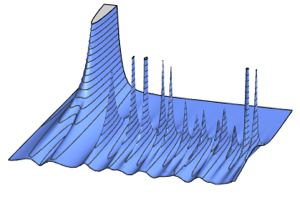
Eigenwert-Abstände von Gaußschen Verteilungen

Die Abstände benachbarter Eigenwerte von Matrixverteilungen besitzen eine gemeinsame Grenzform der Abstandsverteilung, die in vielen Systemen der Natur auftritt, wie zum Beispiel beim Abstand zwischen benachbarten Energieniveaus schwerer Atome.

Berechnen Sie die Eigenwert-Abstände von 2×2 Matritzen von unterschiedlichen Gaußschen Ensembles.

In[1]:=

gaussiandists = {GaussianOrthogonalMatrixDistribution[2], GaussianUnitaryMatrixDistribution[2], GaussianSymplecticMatrixDistribution[2]};

In[2]:=

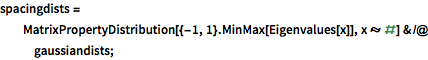
spacingdists = MatrixPropertyDistribution[{-1, 1}.MinMax[Eigenvalues[x]], x \[Distributed] #] & /@ gaussiandists;

In[3]:=

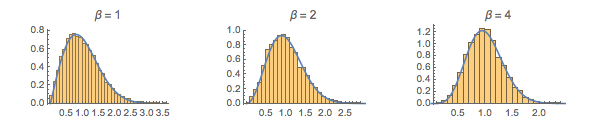
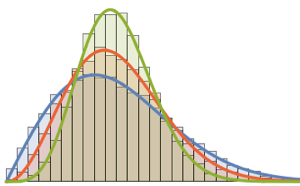
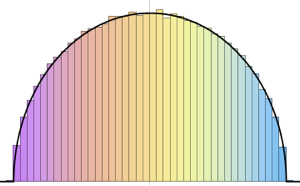
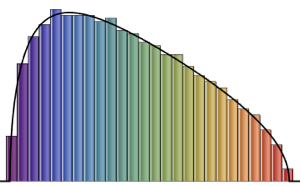
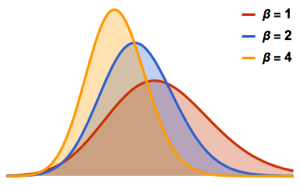
gaps = Normalize[RandomVariate[#, 10000], Mean] & /@ spacingdists;

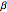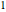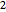Vergleichen Sie die Histogramme für jede Verteilung mit ihrer geschlossenen Form, auch bekannt als die Wignersche Vermutung von , und .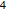

In[4]:=

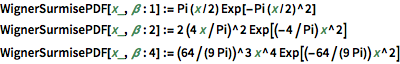
WignerSurmisePDF[x_, \[Beta] : 1] := Pi (x/2) Exp[-Pi (x/2)^2] WignerSurmisePDF[x_, \[Beta] : 2] := 2 (4 x/Pi)^2 Exp[(-4/Pi) x^2] WignerSurmisePDF[ x_, \[Beta] : 4] := (64/(9 Pi))^3 x^4 Exp[(-64/(9 Pi)) x^2]

In[5]:=

histogram = Histogram[#, {0.1}, PDF] & /@ gaps; plot = Plot[WignerSurmisePDF[x, #] , {x, 0, 3}] & /@ {1, 2, 4}; GraphicsRow@ MapThread[ Show[#1, #2, ImageSize -> 180, PlotLabel -> Row[{"\[Beta] = ", #3}]] &, {histogram, plot, {1, 2, 4}}]

Out[5]=