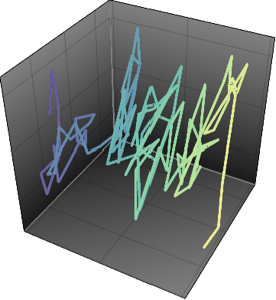
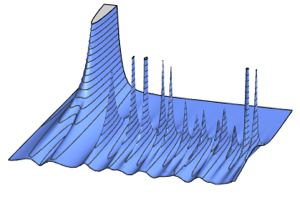
Spektrale Leistungsdichte einer Matrix

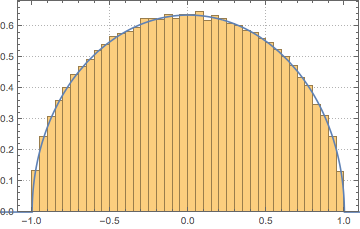
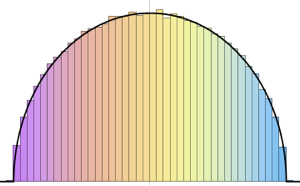
Die multivariate spektrale Leistungsdichte mehrerer Matrixverteilungen besitzt eine entsprechende gemeinsame Grenzform. Bei hermiteschen Zufallsmatritzen mit unabhängigen Einträgen ist dies das Wignersche Halbkreisgesetz.

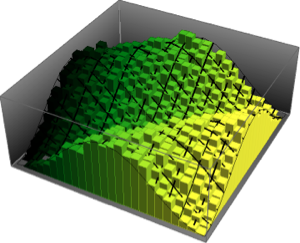
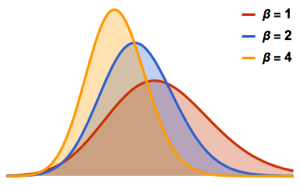
Bei Gaußschen Ensembles hat die skalierte spektrale Leistungsdichte der Matritzen in finiten Matrixdimensionen eine geschlossene Form, in Zusammenhang mit den Eigenfunktionen des harmonischen Oszillators in der Quantenmechanik.

Verwenden Sie MatrixPropertyDistribution, um das skalierte Spektrum des Gaußschen Einheitsensembles zu repräsentieren und den geschlossenen Ausdruck ihrer multivariaten spektralen Leistungsdichte anzugeben.

In[1]:=

scaledSpectrum\[ScriptCapitalD][n_] := MatrixPropertyDistribution[ Eigenvalues[\[Lambda]]/(2 Sqrt[n]), \[Lambda] \[Distributed] GaussianUnitaryMatrixDistribution[n]];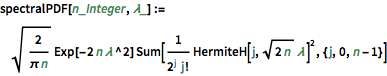

In[2]:=

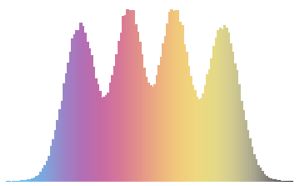
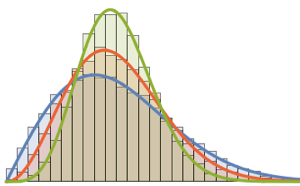
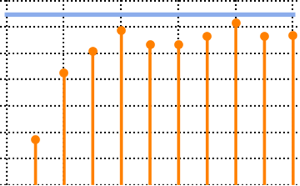
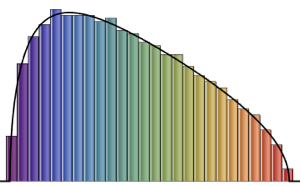
spectralPDF[n_Integer, \[Lambda]_] := Sqrt[2/(\[Pi] n)] Exp[-2 n \[Lambda]^2] Sum[ 1/(2^j j!) HermiteH[j, Sqrt[2 n] \[Lambda]]^2, {j, 0, n - 1}]

Bei kleinen Matrixdimensionen tritt ein oszillierendes Muster auf, wobei die Anzahl von Dichtemaxima der Matrixgröße gleicht.

In[3]:=

scaledSpectra = Flatten[RandomVariate[scaledSpectrum\[ScriptCapitalD][#], 10^5]] & /@ {3, 4, 5};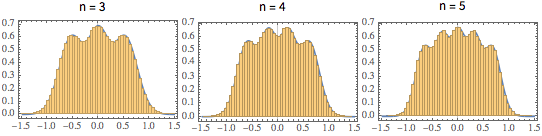

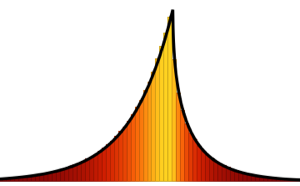
In[4]:=

Row@MapThread[ Show[Plot[spectralPDF[#1, x], {x, -1.5, 1.5}, PlotTheme -> "Scientific", PlotStyle -> ColorData[97, 1], PlotLegends -> Placed["n = " <> ToString@#1, Above]], Histogram[#2, {0.05}, PDF]] &, {{3, 4, 5}, scaledSpectra}]

Out[4]=

Bei großen Dimension konvergiert die Dichte gegen WignerSemicircleDistribution.

In[5]:=

n = 250; scaledSpectrum = Flatten[RandomVariate[scaledSpectrum\[ScriptCapitalD][n], 10^2]];

In[6]:=

Show[Histogram[scaledSpectrum, {0.05}, PDF, PlotTheme -> "Detailed"], Plot[PDF[WignerSemicircleDistribution[1], x], {x, -1.5, 1.5}, Exclusions -> None, PlotTheme -> "Scientific", PlotLegends -> None, PlotStyle -> ColorData[97, 1]], ImageSize -> Medium]

Out[6]=