Marchenko–Pastur-Verteilung

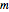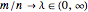Die Marchenko–Pastur-Verteilung ist die Grenzverteilung von Eigenwerten von Wishart-Matritzen, wenn die Matrixdimension u Freiheitsgrade im Verhältnis gegen unendlich tendieren. Bei 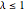hat die Verteilung keine Punktmasse und die Wahrscheinlichkeitsdichtefunktion ist wohldefiniert.

In[1]:=

PDF[MarchenkoPasturDistribution[1/2], x]

Out[1]=

In[2]:=

Plot[PDF[MarchenkoPasturDistribution[1/2], x], {x, 0, 3}, PlotRange -> All, Exclusions -> None, Filling -> Axis, PlotTheme -> "Detailed", ImageSize -> Medium, PlotLegends -> None]

Out[2]=

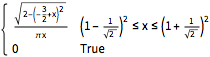
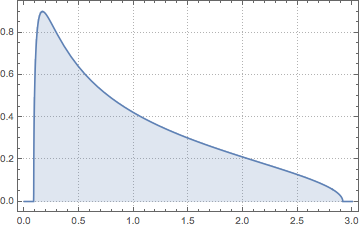
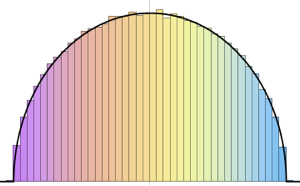
Nehmen Sie eine Wishart-Verteilung mit einer skalierten Einheitsmatrix und berechnen Sie die skalierten Eigenwerte.

In[3]:=

n = 10^4; m = 10^3; eigs = RandomVariate[ MatrixPropertyDistribution[Eigenvalues[x]/n, x \[Distributed] WishartMatrixDistribution[n, IdentityMatrix[m]]]];

Berechnen Sie das Ergebnis mit der Marchenko–Pastur-Dichtefunktion.

In[4]:=

Show[Histogram[eigs, {0.05}, "PDF", ImageSize -> Medium, PlotTheme -> "Detailed"], Plot[PDF[MarchenkoPasturDistribution[m/n], x], {x, 0, 1.8}, PlotTheme -> "Detailed", PlotLegends -> None, Exclusions -> None]]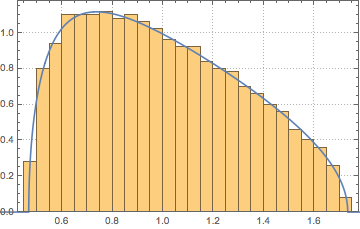

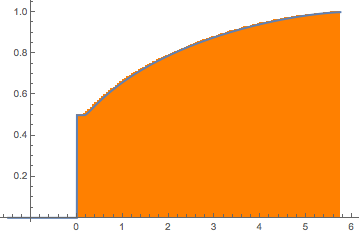
Out[4]=

Bei 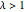ist die Wishart-Matrix singulär. Mit der Wahrscheinlichkeit 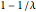hat die Verteilung eine Punktmasse bei .

In[5]:=

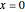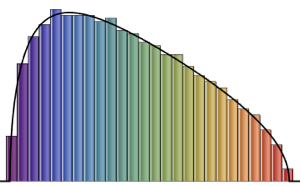
m = 500; n = 2 m; CDF[MarchenkoPasturDistribution[n/m], 0]

Out[5]=

Generieren Sie eine singuläre Wishart-Matrix mit Einheitskovarianz und berechnen Sie die skalierten Eigenwerte.

In[6]:=

matrix = Transpose[#].# &[RandomVariate[NormalDistribution[], {m, n}]]; eigvs = Chop[Eigenvalues[matrix]/m];

Es besteht eine Lücke in der Dichte der Eigenwerte nahe 0 und die Klasse bei 0 besitzt große Dichte.

In[7]:=

Histogram[eigvs, {0.05}, PDF, PlotRange -> 1, ChartStyle -> Orange, ImageSize -> Medium]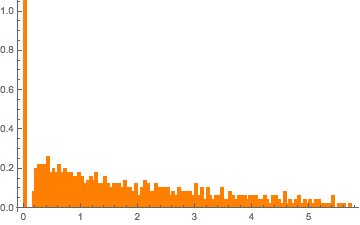

Out[7]=

Passen Sie eine MarchenkoPasturDistribution an die Eigenwerte an.

In[8]:=

edist = EstimatedDistribution[eigvs, MarchenkoPasturDistribution[\[Lambda], 1]]

Out[8]=

Die kumulative Verteilungsfunktion der angepassten Verteilung zeigt eine Sprungstelle am Ursprung.

In[9]:=

Show[Histogram[eigvs, {0.05}, CDF, ChartStyle -> Orange], Quiet@Plot[CDF[edist, x], {x, -1.5, 5.75}, Exclusions -> None, PlotStyle -> Thick], ImageSize -> Medium, AxesOrigin -> {-1, 0}, PlotRange -> {{-1.5, 6}, {0, 1}}]

Out[9]=