Densidad espectral de una matriz
La densidad espectral conjunta de muchas distribuciones de matriz tiene una forma correspondiente universal de límite. Para las matrices aleatorias hermitianas con entradas independientes, esta es la ley de semicírculo de Wigner.
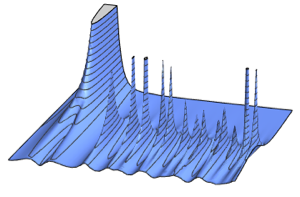
Para los conjuntos de Gauss, la densidad espectral de las matrices tiene una forma cerrada para la dimensión de matriz finita, relacionada con las funciones propias del oscilador armónico cuántico.
Use MatrixPropertyDistribution para representar el espectro escalado del conjunto unitario de Gauss y proporcione la expresión de forma cerrada de su densidad espectral conjunta.

scaledSpectrum\[ScriptCapitalD][n_] :=
MatrixPropertyDistribution[
Eigenvalues[\[Lambda]]/(2 Sqrt[n]), \[Lambda] \[Distributed]
GaussianUnitaryMatrixDistribution[n]];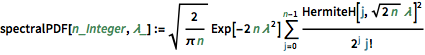
spectralPDF[n_Integer, \[Lambda]_] :=
Sqrt[2/(\[Pi] n)] Exp[-2 n \[Lambda]^2] \!\(
\*UnderoverscriptBox[\(\[Sum]\), \(j = 0\), \(n - 1\)]
\*FractionBox[
SuperscriptBox[\(HermiteH[j,
\*SqrtBox[\(2\ n\)]\ \[Lambda]]\), \(2\)], \(
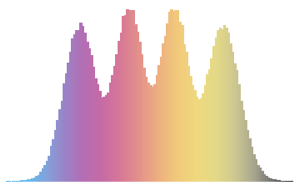
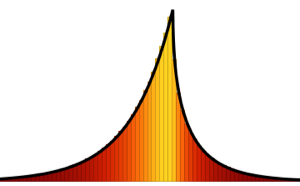
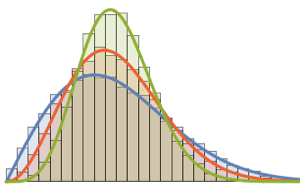
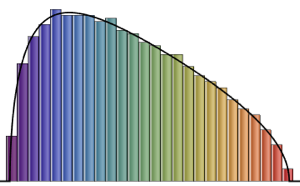
\*SuperscriptBox[\(2\), \(j\)]\ \(j!\)\)]\)Para la distribución de matriz pequeña, hay un patrón oscilatorio de características, cuyo número de densidad máxima es igual al tamaño de la matriz.
scaledSpectra =
Flatten[RandomVariate[scaledSpectrum\[ScriptCapitalD][#],
10^5]] & /@ {3, 4, 5};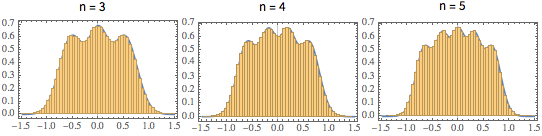
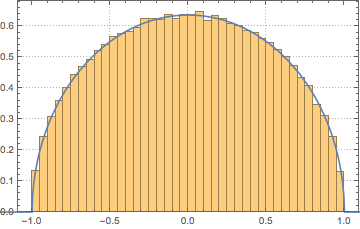
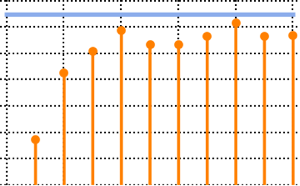
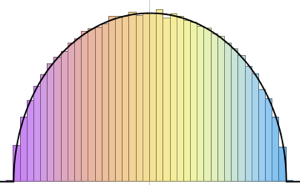
En el límite de la dimensión grande, la densidad converge con WignerSemicircleDistribution.
n = 250;
scaledSpectrum =
Flatten[RandomVariate[scaledSpectrum\[ScriptCapitalD][n], 10^2]];