Movimiento browniano en CUE
El movimiento browniano en el distribuidor de matrices unitarias puede ser construido por generadores infinitesimales de un conjunto unitario de Gauss. La distribución estacionaria de este movimiento browniano es entonces idéntica a la distribución de CUE.
In[1]:=
mats = RandomVariate[GaussianUnitaryMatrixDistribution[0.1, 2],
100000];
mats = Table[MatrixExp[I mat], {mat, mats}];Genere una ruta browniana con el punto inicial de la muestra de CUE.
In[2]:=
initial = RandomVariate[CircularUnitaryMatrixDistribution[2]];
res = FoldList[#2.#1 &, initial, mats];Calcule las fase de valores propios y compárelos con la función de densidad de probabilidad de las matrices de valores propios de CUE.
In[3]:=
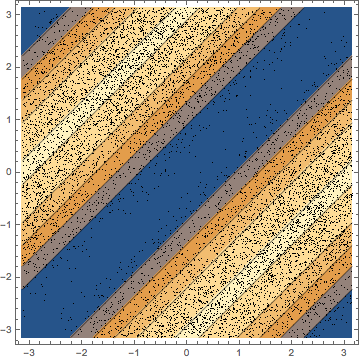
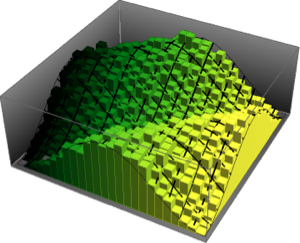
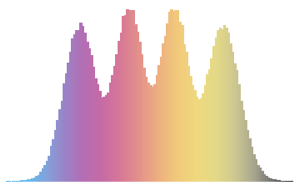
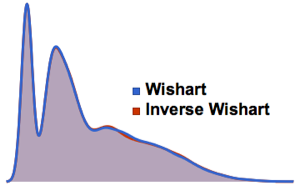
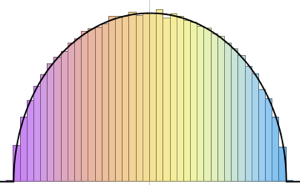
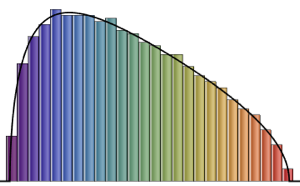
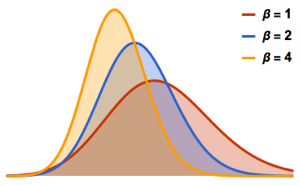
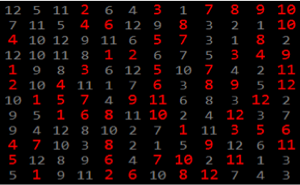
phases = RandomSample /@ Arg[Eigenvalues /@ res];muestre la entrada completa de Wolfram Language
Out[4]=