Rotaciones aleatorias

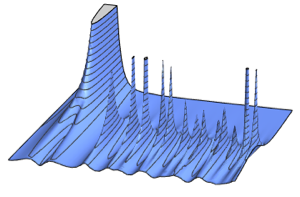
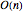CircularRealMatrixDistribution representa una distribución uniforme de las matrices cuadradas octogonales de dimensión , también conocidas como la medida de Haar en el grupo ortogonal . Las matrices generadas de acuerdo con esta distribución pueden actuar como operadores de rotación de vectores en un espacio vectorial -dimensional

Defina una distribución de vectores aleatorios obtenidos rotando un vector en 3D fijo (0,0,1) por una matriz aleatoria de CircularRealMatrixDistribution de dimensión 3.

In[1]:=

\[ScriptCapitalD] = MatrixPropertyDistribution[r.{0, 0, 1}, r \[Distributed] CircularRealMatrixDistribution[3]];

Use esta distribución para tomar muestra de puntos en la superficie de la unidad de esfera.

In[2]:=

points = RandomVariate[\[ScriptCapitalD], 10^3];

Compruebe si todos los puntos de muestra pertenecen a la unidad de esfera.

In[3]:=

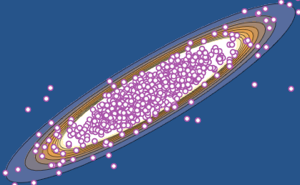
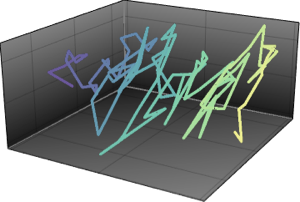
AllTrue[points, RegionMember[Sphere[3]]]

Out[3]=

Represente gráficamente los puntos muestreados con el vector original.

In[4]:=

Graphics3D[{{Gray, PointSize[Small], Point[points]}, {Red, Thick, Arrow[{{0, 0, 0}, {0, 0, 1}}]}}, Axes -> True]

Out[4]=

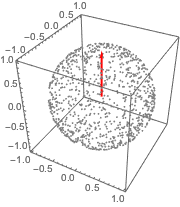
El elemento del área de superficie en la esfera en coordinadas cilíndricas es dado por .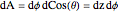

In[5]:=

{x, y, z} = Transpose[points]; \[Phi] = ArcTan[y/x];

Compruebe si las distribuciones marginales de 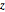y 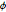son uniformes.

In[6]:=

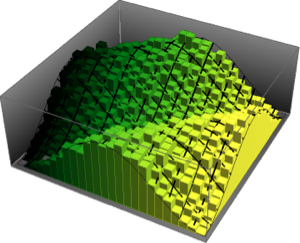
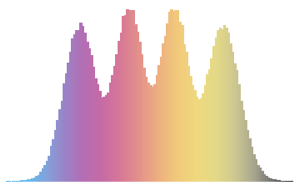
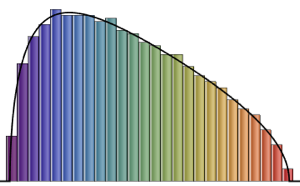
Histogram[#, 20, PDF] & /@ {\[Phi], z}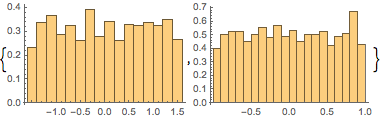

Out[6]=

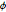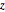Revise si los puntos de muestra están distribuidos uniformemente en la superficie de la esfera, comprobando si la distribución conjunta de y es uniforme.

In[7]:=

Graphics[Point[Transpose[{\[Phi], z}]], Axes -> True, AxesOrigin -> {-\[Pi]/2, -1}, AxesLabel -> {"\[Phi]", "z"}]

Out[7]=

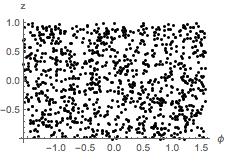
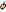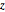Pruebe la hipótesis de que la distribución conjunta de y es uniforme.

In[8]:=

DistributionFitTest[Transpose[{\[Phi], z}], UniformDistribution[{{-Pi/2, Pi/2}, {-1, 1}}], "TestConclusion"]

Out[8]=