Wolfram Language™

Conjuntos circulares (COE, CUE, ...)

Los conjuntos circulares son familias de matrices unitarias con distribuciones invariantes bajo distintas transformaciones unitarias. Las aplicaciones típicas están en mecánica estadística, teoría de números, combinatoria y física nuclear.

Las matrices de un conjunto circular real (CRE) son ortogonales. »

In[1]:=

cre = RandomVariate[CircularRealMatrixDistribution[5]];

In[2]:=

OrthogonalMatrixQ[cre]

Out[2]=

Las matrices de un conjunto circular unitario (CUE) son unitarias. »

In[3]:=

cue = RandomVariate[CircularUnitaryMatrixDistribution[5]];

In[4]:=

UnitaryMatrixQ[cue]

Out[4]=

Las matrices de un conjunto circular ortogonal (COE) son simétricas y unitarias. »

In[5]:=

coe = RandomVariate[CircularOrthogonalMatrixDistribution[5]];

In[6]:=

SymmetricMatrixQ[coe] && UnitaryMatrixQ[coe]

Out[6]=

Las matrices de un conjunto simpléctico circular (CSE) son auto-duales cuaterniónicas unitarias. »

In[7]:=

selfdualQuaternionicQ[m_] := With[{\[ScriptCapitalJ] = KroneckerProduct[{{0, -1}, {1, 0}}, IdentityMatrix[Length[m]/2]], mat = SetAccuracy[m, 10]}, Transpose[mat].\[ScriptCapitalJ] == \[ScriptCapitalJ].mat];

In[8]:=

cse = RandomVariate[CircularSymplecticMatrixDistribution[5]];

In[9]:=

UnitaryMatrixQ[cse] && selfdualQuaternionicQ[cse]

Out[9]=

Las matrices de un conjunto circular cuaterniónico (CQE) son simplécticas unitarias. »

In[10]:=

symplecticMatrixQ[mat_] := With[{\[ScriptCapitalJ] = KroneckerProduct[{{0, -1}, {1, 0}}, IdentityMatrix[Length[mat]/2]] }, Conjugate[mat].\[ScriptCapitalJ] == \[ScriptCapitalJ].mat];

In[11]:=

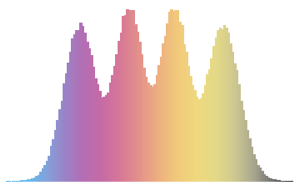
cqe = RandomVariate[CircularQuaternionMatrixDistribution[5]];

In[12]:=

UnitaryMatrixQ[cqe] && symplecticMatrixQ[cqe]

Out[12]=

Los valores propios de matrices de CUE, COE y CSE tienen unidad de longitud y están distribuidas uniformemente en una fase.

In[13]:=

args = Flatten[ Arg[RandomVariate[ MatrixPropertyDistribution[Eigenvalues[x], x \[Distributed] #], 10^4]]] & /@ {CircularUnitaryMatrixDistribution[5], CircularOrthogonalMatrixDistribution[5], CircularSymplecticMatrixDistribution[5]}; Row[MapThread[ Histogram[#1, {-Pi, Pi, Pi/10}, Frame -> None, ChartLegends -> Placed[#2, Above]] &, {args, {Style["Unitary", 15], Style["Orthogonal", 15], Style["Symplectic", 15]}}]]

Out[13]=

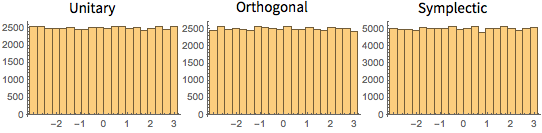
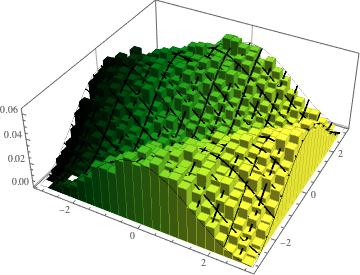
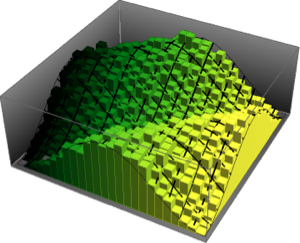
Visualice la distribución conjunta de la fase de los valores propios de una CUE bidimensional y compárela con la densidad actual.

In[14]:=

evs\[ScriptCapitalD] = MatrixPropertyDistribution[Arg[Eigenvalues[x]], x \[Distributed] CircularUnitaryMatrixDistribution[2]]; \[CurlyPhi]s = RandomSample /@ RandomVariate[evs\[ScriptCapitalD], 10^5];

In[14]:=

Show[ Histogram3D[\[CurlyPhi]s, {-Pi, Pi, 0.25}, PDF, PlotTheme -> "Scientific", ChartStyle -> "AvocadoColors"], Plot3D[1/(8 Pi^2) Abs[Exp[I \[Phi]1] - Exp[I \[Phi]2]]^2, {\[Phi]1, -Pi, Pi}, {\[Phi]2, -Pi, Pi}, PlotStyle -> None, MeshStyle -> Thick], ImageSize -> Medium]

Out[15]=