Wolfram言語™

ウィシャート分布と逆ウィシャート分布

ウィシャート分布は，独立多変量正規ランダムベクトルから取り出されたサンプルの共分散行列の分布である．これは 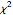分布を多次元に一般化したものである．分布は当然ながら多変量統計（回帰，共分散等）で使用されている．

ランダム正定値行列を生成し，ウィシャート分布の母数として使用する．

In[1]:=

\[CapitalSigma] = DiagonalMatrix[RandomReal[10, 5]];

ウィシャート分布の行列は対称正定値行列である． »

In[2]:=

dist = WishartMatrixDistribution[30, \[CapitalSigma]]; mat = RandomVariate[dist];

In[3]:=

SymmetricMatrixQ[mat] && PositiveDefiniteMatrixQ[mat]

Out[3]=

逆ウィシャート分布はウィシャート分布の逆行列の分布である． »

In[4]:=

invdist = InverseWishartMatrixDistribution[30, Inverse[\[CapitalSigma]]]; invmat = RandomVariate[invdist];

逆ウィシャート分布の行列は対称正定値行列である．

In[5]:=

SymmetricMatrixQ[invmat] && PositiveDefiniteMatrixQ[invmat]

Out[5]=

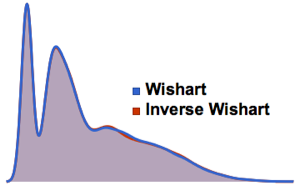
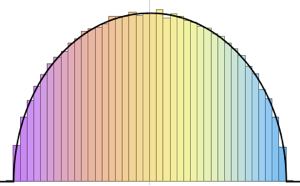
ウィシャート分布と逆ウィシャート分布の行列の固有値の分布を比較する．

In[6]:=

eigs = Flatten[ RandomVariate[ MatrixPropertyDistribution[Eigenvalues[x], x \[Distributed] dist], 10^4]]; inveigs = Flatten[RandomVariate[ MatrixPropertyDistribution[Eigenvalues[x]^-1, x \[Distributed] invdist], 10^4]];

In[7]:=

SmoothHistogram[{eigs, inveigs}, PlotLegends -> {"Wishart", "Inverse Wishart"}, Filling -> Axis, ImageSize -> Medium, PlotTheme -> "Scientific"]

Out[7]=

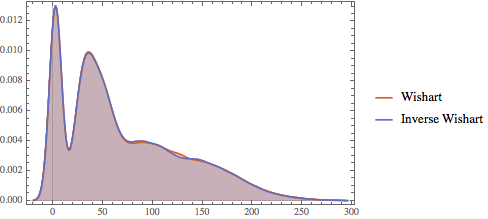
任意の非零ベクトル 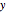と，スケール行列が 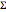であるウィシャート行列 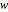について，統計 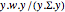は 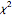分布である．

In[8]:=

y = #/Sqrt[#.\[CapitalSigma].#] &[RandomReal[1, 5]]; data = RandomVariate[ MatrixPropertyDistribution[y.w.y, w \[Distributed] WishartMatrixDistribution[30, \[CapitalSigma]]], 10^4];

In[9]:=

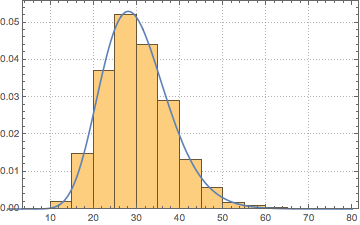
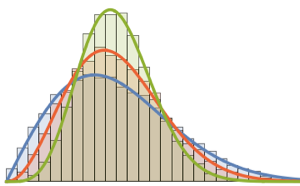
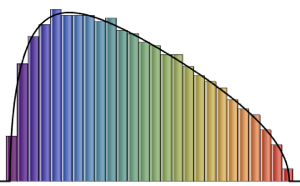
Show[Histogram[data, Automatic, PDF, PlotTheme -> "Detailed"], Plot[PDF[ChiSquareDistribution[30], x], {x, 0, 80}], ImageSize -> Medium]

Out[9]=