한 자루의 동전의 견적

한 자루의 미국 동전이 은행에서 도난당했습니다. 그 자루를 열지 않고 자루 속 통화의 가격을 알아낼 수 있을까요? 한가지 분명히 알 수 있는 물리적 특징은 그 자루의 무게일 것입니다. 동전이 든 가방의 무게가 1파운드라 가정하고, Wolfram Knowledgebase의 임베디드 기능을 통해 통화에 대해 알려진 정보를 가지고 선형 방정식 해결 기능을 사용하여 도난된 동전의 예상 값을 구할 수 있습니다.

먼저, 간접적으로 정의된 엔티티 클래스를 사용하여 현재 통용되는 미국 동전의 목록을 반환합니다.

In[1]:=

EntityClass["CurrencyDenomination", {EntityProperty[ "CurrencyDenomination", "IssuingCountry"] -> Entity["Country", "UnitedStates"], EntityProperty["CurrencyDenomination", "Format"] -> "coin"}]

Out[1]=

[+]를 클릭하여 간접적으로 정의된 엔티티 클래스를 확장하고, 그 멤버를 찾고 동전의 가치에 따라 정렬합니다.

In[2]:=

coinsUS = EntityList[ EntityClass[ "CurrencyDenomination", { EntityProperty[ "CurrencyDenomination", "IssuingCountry"] -> Entity[ "Country", "UnitedStates"], EntityProperty["CurrencyDenomination", "Format"] -> "coin"}]] // SortBy[#[EntityProperty["CurrencyDenomination", "Value"]] &]

Out[2]=

동전의 사진 콜라주를 만듭니다.

In[3]:=

ImageCollage[ EntityValue[coinsUS, EntityProperty["CurrencyDenomination", "Image"]], Background -> White]

Out[3]=

동전의 특성을 테이블에 정리합니다.

In[4]:=

TextGrid[{ImageResize[#2, 60], #1, Row[Riffle[#3, Style[" | ", Gray]]]} & @@@ EntityValue[ coinsUS, {EntityProperty["CurrencyDenomination", "Entity"], EntityProperty["CurrencyDenomination", "Image"], EntityProperty["CurrencyDenomination", "PeopleOnCurrency"]}], Alignment -> {Left, Center}, Dividers -> All] // TraditionalForm

Out[4]//TraditionalForm=

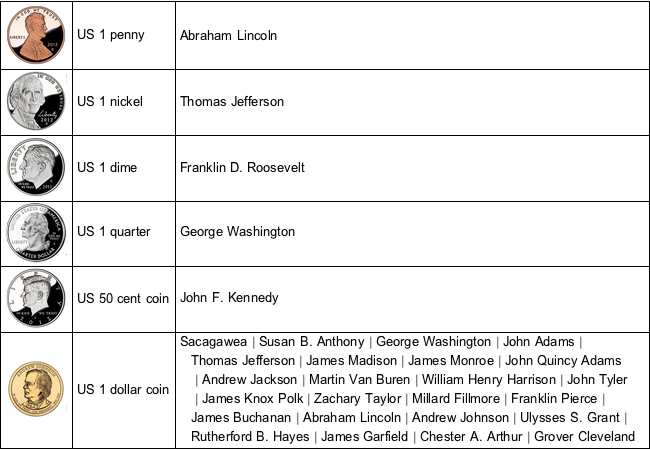
동전의 금액 (센트)과 질량 (g)을 찾고, 질량을 유리수로 변환합니다.

In[5]:=

{values, masses} = Transpose[EntityValue[coinsUS, {"Value", "Weight"}]]

Out[5]=

In[6]:=

coinsandweights = Transpose[{ QuantityMagnitude[UnitConvert[values, "USCents"]], Rationalize[QuantityMagnitude[N[UnitConvert[masses, "Grams"]]]] }]

Out[6]=

In[7]:=

lcm = LCM @@ Denominator[Rationalize[coinsandweights][[All, 2]]];

In[8]:=

rationalcoinweights = lcm #2 & @@@ Rationalize[coinsandweights]

Out[8]=

1 파운드의 무게와 호환하는 동전의 모든 분포를 (가방의 무게는 무시할 수 있는 정도라 할때) ± 0.1%의 오차로 구합니다.

In[9]:=

meanWeight = QuantityMagnitude[UnitConvert[Quantity[1, "Pounds"], "Grams"]];

In[10]:=

error = Normal[Quantity[0.1, "Percent"]];

In[11]:=

{minScaledWeight, maxScaledWeight} = {Floor[lcm meanWeight (1 - error/2)], Ceiling[lcm meanWeight (1 + error/2)]}

Out[11]=

FrobeniusSolve를 사용하여 필요한 무게가 될 수 있는 모든 가능한 동전 집합을 조사합니다.

In[12]:=

allSolutions = Monitor[ Table[fb = FrobeniusSolve[rationalcoinweights, scaledweight], {scaledweight, minScaledWeight, maxScaledWeight}], Row[{NumberForm[ 100. (scaledweight - minScaledWeight)/(maxScaledWeight - minScaledWeight), {4, 1}, "NumberPadding" -> {" ", "0"}], "%: ", Length[fb], " solutions"}] ];

In[13]:=

Flatten[allSolutions, 1] // Length

Out[13]=

가방 안 동전의 최소값, 중앙값, 평균값, 최대값을 (어떤 조합도 동일한 수준으로 일어날 수 있다고 가정) 구합니다.

In[14]:=

coins = coinsandweights[[All, 1]];

In[15]:=

dollarValues = (coins.#/100.) & /@ Flatten[allSolutions, 1];

In[16]:=

TextGrid[With[{stats = {Min, Median, Mean, Max}}, Transpose[{stats, NumberForm[Quantity[#, "USDollars"], {\[Infinity], 2}] & /@ Through[stats[dollarValues]]}]], Alignment -> {{Left, Decimal}}, Dividers -> All, Background -> {Automatic, {{LightBlue, None}}}] // TraditionalForm

Out[16]//TraditionalForm=

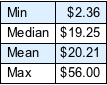
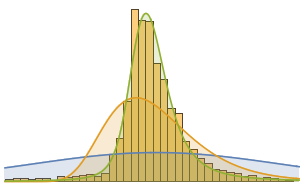
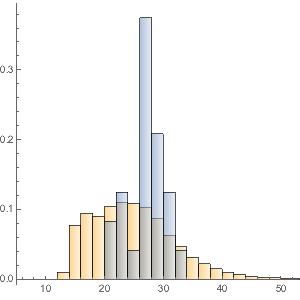
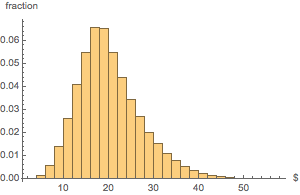
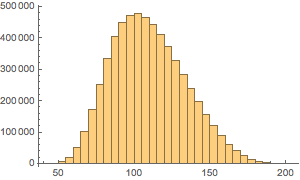
총 금액 분포의 히스토그램을 작성합니다.

In[17]:=

Histogram[dollarValues, Automatic, "PDF", AxesLabel -> {Quantity[None, "USDollars"], "fraction"}]

Out[17]=

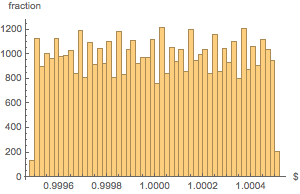
모든 가방의 무게 분포는 매우 균일합니다.

In[18]:=

weights = coinsandweights[[All, -1]]; lbg = QuantityMagnitude[UnitConvert[Quantity[1, "Pounds"], "Grams"]]; weightvalues = (weights.#)/lbg & /@ Flatten[allSolutions, 1];

In[19]:=

Histogram[weightvalues, 50, "PDF", AxesLabel -> {Quantity[None, "USDollars"], "fraction"}]

Out[19]=

동전의 수의 분포를 플롯합니다.

In[20]:=

Histogram[Total /@ Flatten[allSolutions, 1], {5}]

Out[20]=

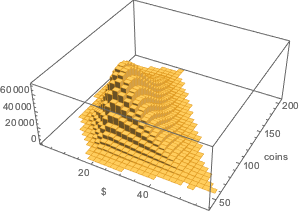
금액 대 동전 자루의 수의 2변량 분포를 알아봅니다.

In[21]:=

Histogram3D[{coins.#/100., Total[#]} & /@ Flatten[allSolutions, 1], AxesLabel -> {Quantity[None, "USDollars"], "coins"}]

Out[21]=