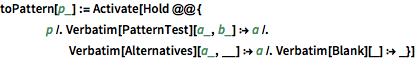Função especial de rede de derivadas

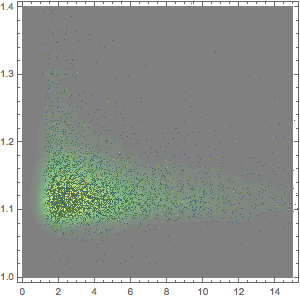
A Wolfram Language contém mais de 300 funções matemáticas integradas. Considere a operação de diferenciação aplicada a cada uma destas funções. Na maioria dos casos, uma ou mais novas funções aparecem nas derivadas resultantes. A quantificação das conexões resulta em um estudo interessante sobre a relação entre os símbolos e operações sobre elas. Em particular, o exemplo a seguir deriva da rede que surge da diferenciação de ordem inferior.

Conforme aprendido em cálculo elementar, diferenciar o logaritmo natural resulta uma função inversa.

In[1]:=

D[Log[x], x]

Out[1]=

Por outro lado, para algumas funções, uma derivada pode ser expressa diretamente através da função original.

In[2]:=

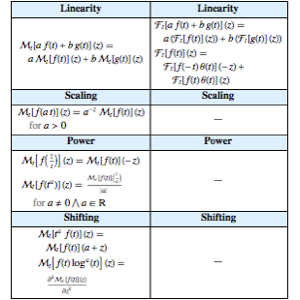
D[ProductLog[x], x]

Out[2]=

A propriedade "LowOrderDerivatives" de MathematicalFunctionData oferece acesso rápido e conveniente a todas as derivadas.

In[3]:=

Entity["MathematicalFunction", "EllipticF"][ EntityProperty["MathematicalFunction", "LowOrderDerivatives"]] // TraditionalForm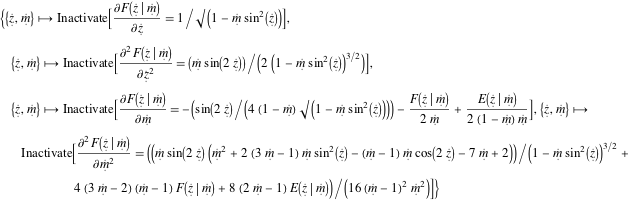

Out[3]//TraditionalForm=

Colete todas as funções e seus padrões de argumento para identificar a função após a diferenciação. (Para evitar ocorrências comuns de potências, não busque pela potência nem a função de raiz quadrada.) Por exemplo, com base na identidade , a função Sec envolve as funções Tan assim como a ela mesma, resultando em duas conexões.

In[4]:=

allFunctions = DeleteCases[MathematicalFunctionData[], Entity["MathematicalFunction", "Sqrt"] | Entity["MathematicalFunction", "Power"]];

In[5]:=

patts = EntityValue[allFunctions, EntityProperty["MathematicalFunction", "ArgumentPattern"]];

In[6]:=

toPattern[p_] := Activate[Hold @@ { p /. Verbatim[PatternTest][a_, b_] :> a /. Verbatim[Alternatives][a_, __] :> a /. Verbatim[Blank][_] :> _}]

In[7]:=

pairs = {#1, toPattern[#2]} & @@@ Transpose[{allFunctions, patts}];

In[8]:=

(identify[#2] = #1) & @@@ pairs;

In[9]:=

makeConnection[f1_, id_] := Module[{indices, heldSubexpressions, f2List, \[ScriptCapitalF]\[GothicCapitalF]}, indices = Quiet[Cases[ MapIndexed[\[ScriptCapitalF]\[GothicCapitalF], id, {0, \[Infinity]}], _\[ScriptCapitalF]\[GothicCapitalF], \ \[Infinity]][[All, -1]]]; heldSubexpressions = Union[Extract[id, indices, Hold]]; f2List = Union[Last /@ DeleteCases[({#1, identify[#1]} & /@ heldSubexpressions), {_, _identify}]]; {f1 \[DirectedEdge] #, id /. HoldPattern[Function[_, Inactivate[x_]]] :> HoldForm[x]} & /@ f2List]

In[10]:=

makeConnection[Entity["MathematicalFunction", "Sec"] , Function[{x}, Inactivate[D[Sec[x], x] == Sec[x] Tan[x]]]]

Out[10]=

Analise todas as derivadas, elimine todas as reincidências nos gráficos resultantes e visualize a estrutura gráfica resultante.

In[11]:=

\[Lambda]F = Length[allFunctions]; Monitor[ allConnections = Table[ fD = allFunctions[[\[ScriptJ]]]; derivatives = Activate[ allFunctions[[\[ScriptJ]]][ EntityProperty["MathematicalFunction", "LowOrderDerivatives"]] /. HoldPattern[Power[E, z_]] :> Exp[z]]; connections = If[derivatives === Missing["NotAvailable"], {}, {#[[1, 1]], SortBy[#[[All, -1]], LeafCount]} & /@ GatherBy[ Flatten[makeConnection[fD, #] & /@ derivatives, 1] // Union, First]], {\[ScriptJ], \[Lambda]F}];, Row[{"function ", \[ScriptJ], " of ", \[Lambda]F, ": ", fD}]];

In[12]:=

gr = Graph[Flatten[allConnections, 1][[All, 1]]]

Out[12]=

Conte o número de conexões.

In[13]:=

Flatten[allConnections, 1] // Length

Out[13]=

Ache as reincidências.

In[14]:=

selfLoops = Select[ConnectedComponents[ Graph[Flatten[allConnections /. DirectedEdge -> UndirectedEdge, 1][[All, 1]]]], Length[#] == 1 &]

Out[14]=

Encontre os grupos de funções que são fechados sob diferenciação e visualize como gráficos legendados.

In[15]:=

smallLoops = Select[ConnectedComponents[ Graph[Flatten[allConnections /. DirectedEdge -> UndirectedEdge, 1][[All, 1]]]], 1 < Length[#] < 20 &];

In[16]:=

Graph[Select[Flatten[allConnections, 1], MemberQ[#, Alternatives @@ Flatten[smallLoops], \[Infinity]] &][[ All, 1]], VertexLabels -> ((# -> MapAt[Nothing &, CommonName[#], {{1, 1}}]) & /@ Union[Flatten[smallLoops]])]

Out[16]=

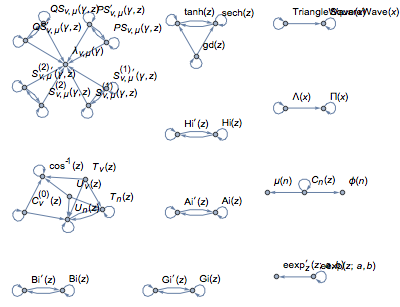
A maioria das funções são parte do componente gigante do gráfico. Passe o mouse sobre os vértices para ver as funções e sobre as bordas para ver as derivadas que conectam as funções.

In[17]:=

allConnectionsRest = Select[Flatten[allConnections, 1], FreeQ[#, Alternatives @@ Flatten[{selfLoops, smallLoops}], \[Infinity]] &];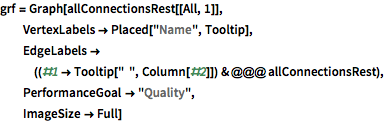

In[18]:=

grf = Graph[allConnectionsRest[[All, 1]], VertexLabels -> Placed["Name", Tooltip], EdgeLabels -> ((#1 -> Tooltip[" ", Column[#2]]) & @@@ allConnectionsRest), PerformanceGoal -> "Quality", ImageSize -> Full]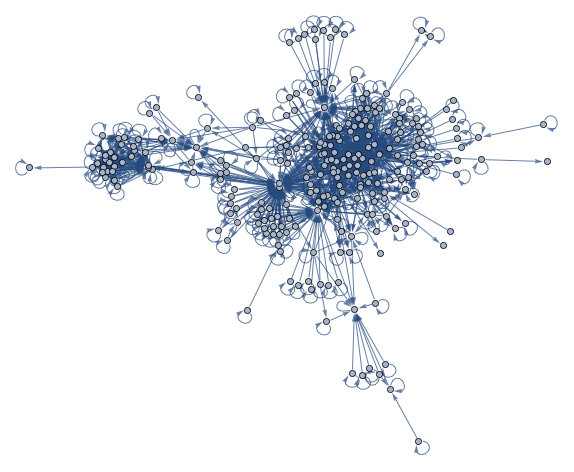

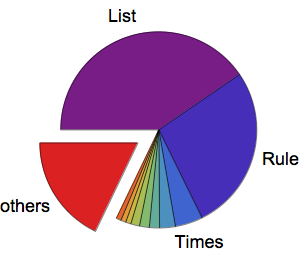
Out[18]=

Dividir o gráfico em comunidades mostra funções elípticas, funções hipergeométrica, funções de janela, funções zeta, e mais alguns grupos de funções.

In[19]:=

CommunityGraphPlot[grf, FindGraphCommunities[grf, Method -> "Modularity"]]

Out[19]=