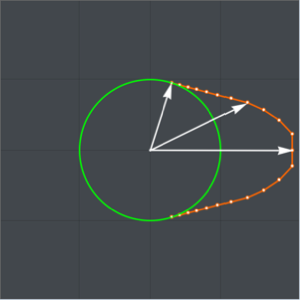
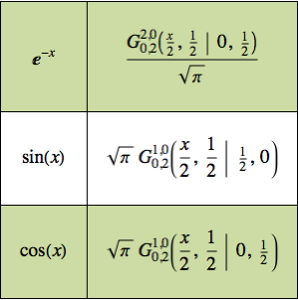Finden Sie das größte kleinste Polygon
Finden Sie unter allen Polygonen mit 
Seiten und Durchmesser 
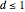das Polygon mit maximalem Flächeninhalt.
In Version 11 können Sie durch FindMinimum mit einem IPOPT-Solver Optimierungsprobleme effizienter lösen.
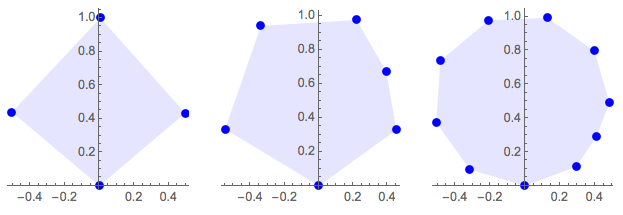
Geben Sie mit n die Zahl der Eckpunkte des Polygons an.
n = 50;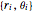 
seien die Polarkoordinaten der 
Ecke des Polygons.
vars = Join[Array[r, n], Array[\[Theta], n]];Sie erfüllen die Bedingungen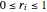 
, 
, 
, 
.
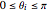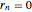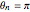varbounds =
Join[Table[0 <= r[i] <= 1, {i, n - 1}], {r[n] == 0},
Table[0 <= \[Theta][i] <= Pi, {i, n - 1}], {\[Theta][n] == Pi}];Die Fläche des Polygons ist die Summe der Flächeninhalte von Dreiecken mit den Eckpunkten 
, 
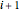und 
(Ursprung).
area = 1/2 Sum[
r[i] r[i + 1] Sin[\[Theta][i + 1] - \[Theta][i]], {i, 1, n - 1}];Der Abstand zwischen jedem zweiten Eckpunkt soll nicht höher als 1 sein.
constr1 =
Flatten[Table[
0 < r[i]^2 + r[j]^2 -
2 r[i] r[j] Cos[\[Theta][i] - \[Theta][j]] <= 1, {i, 1,
n - 1}, {j, i + 1, n}], 2];Aufgrund der Anordnung der Eckpunkte bestehen außerdem die folgenden Bedingungen:
constr2 = Table[\[Theta][i] <= \[Theta][i + 1], {i, 1, n - 1}];Wählen Sie Anfangspunkte für die Variablen.
x0 = vars /. {r[i_] ->
4. i (n + 1 - i)/(n + 1)^2, \[Theta][i_] -> \[Pi] i/n};Maximieren Sie die Flächeninhalte mit Bedingungen.
sol = FindMaximum[{area, constr1, constr2, varbounds},
Thread[{vars, x0}]];Konvertieren Sie das Ergebnis in kartesische Koordinaten.
rectpts =
Table[FromPolarCoordinates[{r[i], \[Theta][i]}], {i, 1, n}] /.
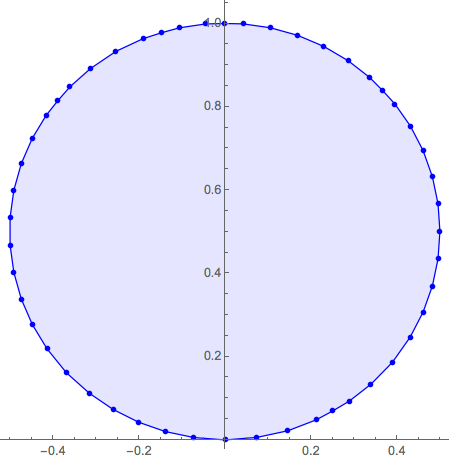
sol[[2]];Visualisieren Sie die Lösung.
Show[ListPlot[rectpts, PlotStyle -> {Blue, PointSize -> Medium}],
Graphics[{Opacity[.1], Blue, EdgeForm[Blue], Polygon[rectpts]}],
AspectRatio -> 1, ImageSize -> Medium]
