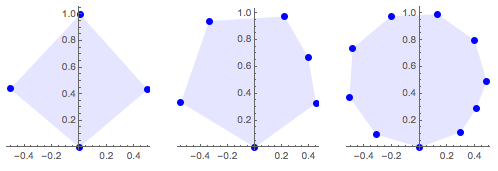
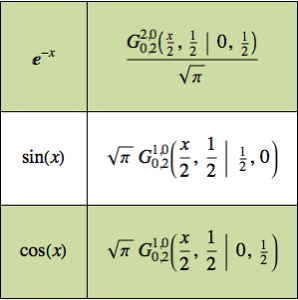面積が最大になる多角形を求める
本の辺を持ち直径が 
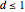の多角形の中から面積が最大になる多角形を求める．
Mathematica 11ではFindMinimumにIPOPTソルバが加わり，大規模な制約条件付き最適化問題がより効率的に解けるようになった．
多角形の頂点の数を n で表す．
In[1]:=
n = 50;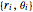
を多角形の第 
番目の頂点の極座標とする．
In[2]:=
vars = Join[Array[r, n], Array[\[Theta], n]];これらは制約条件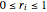
，
，
，
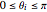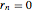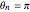を満足する．
In[3]:=
varbounds =
Join[Table[0 <= r[i] <= 1, {i, n - 1}], {r[n] == 0},
Table[0 <= \[Theta][i] <= Pi, {i, n - 1}], {\[Theta][n] == Pi}];多角形の面積は，頂点 
，
， 
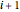（原点）の三角形の面積の和である．
In[4]:=
area = 1/2 Sum[
r[i] r[i + 1] Sin[\[Theta][i + 1] - \[Theta][i]], {i, 1, n - 1}];2頂点間の距離はどれも1を越えてはならない．
In[5]:=
constr1 =
Flatten[Table[
0 < r[i]^2 + r[j]^2 -
2 r[i] r[j] Cos[\[Theta][i] - \[Theta][j]] <= 1, {i, 1,
n - 1}, {j, i + 1, n}], 2];頂点順序があるため，次の制約条件も存在する．
In[6]:=
constr2 = Table[\[Theta][i] <= \[Theta][i + 1], {i, 1, n - 1}];変数の初期点を選ぶ．
In[7]:=
x0 = vars /. {r[i_] ->
4. i (n + 1 - i)/(n + 1)^2, \[Theta][i_] -> \[Pi] i/n};制約条件の対象となる面積を最大化する．
In[8]:=
sol = FindMaximum[{area, constr1, constr2, varbounds},
Thread[{vars, x0}]];直交座標系に変換する．
In[9]:=
rectpts =
Table[FromPolarCoordinates[{r[i], \[Theta][i]}], {i, 1, n}] /.
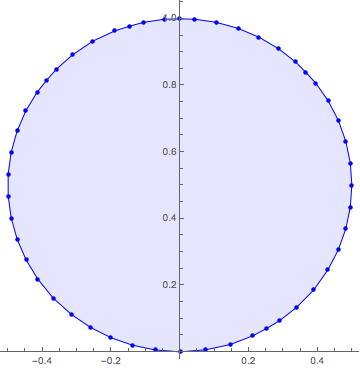
sol[[2]];解をプロットする．
In[10]:=
Show[ListPlot[rectpts, PlotStyle -> {Blue, PointSize -> Medium}],
Graphics[{Opacity[.1], Blue, EdgeForm[Blue], Polygon[rectpts]}],
AspectRatio -> 1, ImageSize -> Medium]Out[10]=
