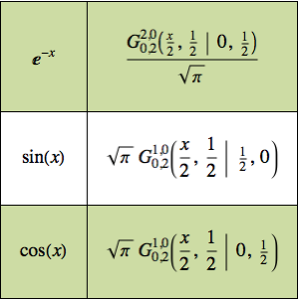Encuentre el polígono pequeño más grande

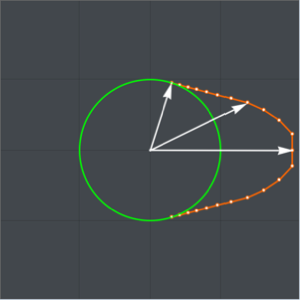
Encuentre el polígono con área máxima entre los polígonos con lados y diámetro .

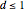En Mathematica 11, FindMinimum agrega un solucionador IPOPT para resolver de forma más eficiente problemas de optimización restringidos a gran escala.

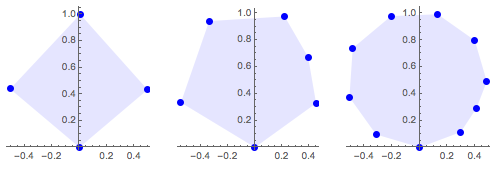
Denote con n el número de vértices del polígono.

In[1]:=

n = 50;

Deje que 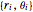sean las coordenadas polares del vértice del polígono .

In[2]:=

vars = Join[Array[r, n], Array[\[Theta], n]];

Estos satisfacen las restricciones , , , .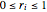

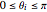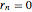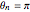In[3]:=

varbounds = Join[Table[0 <= r[i] <= 1, {i, n - 1}], {r[n] == 0}, Table[0 <= \[Theta][i] <= Pi, {i, n - 1}], {\[Theta][n] == Pi}];

El área del polígono es la suma de las áreas de triángulos con vértices , 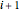y (el origen).

In[4]:=

area = 1/2 Sum[ r[i] r[i + 1] Sin[\[Theta][i + 1] - \[Theta][i]], {i, 1, n - 1}];

La distancia entre cada dos vértices no debería exceder 1.

In[5]:=

constr1 = Flatten[Table[ 0 < r[i]^2 + r[j]^2 - 2 r[i] r[j] Cos[\[Theta][i] - \[Theta][j]] <= 1, {i, 1, n - 1}, {j, i + 1, n}], 2];

Debido al orden de vértices, las siguientes restricciones existen.

In[6]:=

constr2 = Table[\[Theta][i] <= \[Theta][i + 1], {i, 1, n - 1}];

Seleccione puntos iniciales para las variables.

In[7]:=

x0 = vars /. {r[i_] -> 4. i (n + 1 - i)/(n + 1)^2, \[Theta][i_] -> \[Pi] i/n};

Maximice el área sujeta a las restricciones.

In[8]:=

sol = FindMaximum[{area, constr1, constr2, varbounds}, Thread[{vars, x0}]];

Convierta a coordenadas cartesianas.

In[9]:=

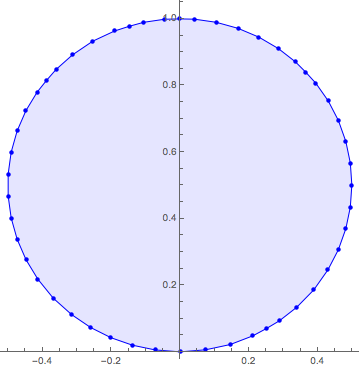
rectpts = Table[FromPolarCoordinates[{r[i], \[Theta][i]}], {i, 1, n}] /. sol[[2]];

Represente gráficamente la solución.

In[10]:=

Show[ListPlot[rectpts, PlotStyle -> {Blue, PointSize -> Medium}], Graphics[{Opacity[.1], Blue, EdgeForm[Blue], Polygon[rectpts]}], AspectRatio -> 1, ImageSize -> Medium]

Out[10]=