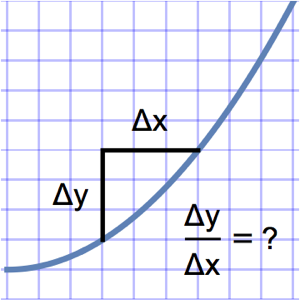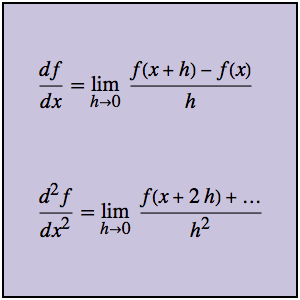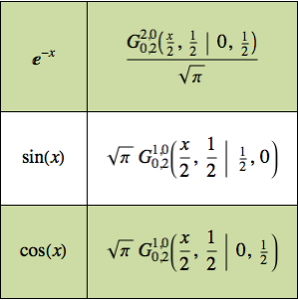Нахождение самого большого маленького многоугольника
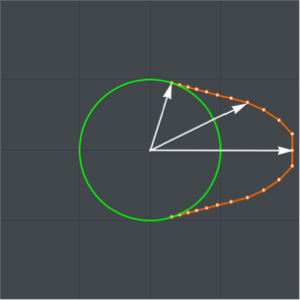
Найти многоугольник с максимальной площадью среди многоугольников с количеством сторон n и диаметром d≤1.
В системе Mathematica 11 функция FindMinimum добавляет устройство для решения задач с оптимизацией внутренних точек. Данная функциональность позволяет решать крупномасштабныe задачи по ограниченной оптимизации более рационально.
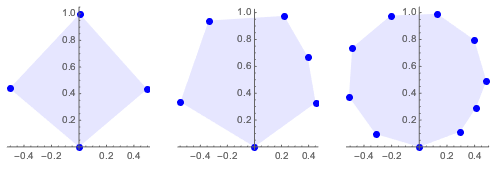
Обозначить с помощью n число вершин многоугольника.
n = 50;Пусть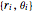 
будут полярными координатами 
-й вершины многоугольника.
vars = Join[Array[r, n], Array[\[Theta], n]];Данные координаты удовлетворяют постоянные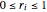 
, 
, 
, 
.
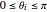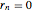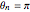varbounds =
Join[Table[0 <= r[i] <= 1, {i, n - 1}], {r[n] == 0},
Table[0 <= \[Theta][i] <= Pi, {i, n - 1}], {\[Theta][n] == Pi}];Площадь многоугольника равна сумме площадей треугольников с вершинами i, i+1 и n.
area = 1/2 Sum[
r[i] r[i + 1] Sin[\[Theta][i + 1] - \[Theta][i]], {i, 1, n - 1}];Расстояние между каждыми двумя вершинами не должно превышать 1.
constr1 =
Flatten[Table[
0 < r[i]^2 + r[j]^2 -
2 r[i] r[j] Cos[\[Theta][i] - \[Theta][j]] <= 1, {i, 1,
n - 1}, {j, i + 1, n}], 2];Благодаря порядку вершин существуют следующие ограничения.
constr2 = Table[\[Theta][i] <= \[Theta][i + 1], {i, 1, n - 1}];Выбрать начальную точку для переменных.
x0 = vars /. {r[i_] ->
4. i (n + 1 - i)/(n + 1)^2, \[Theta][i_] -> \[Pi] i/n};Максимально увеличить площадь объекта до ограничений.
sol = FindMaximum[{area, constr1, constr2, varbounds},
Thread[{vars, x0}]];Перевести полученные значения в декартовы координаты.
rectpts =
Table[FromPolarCoordinates[{r[i], \[Theta][i]}], {i, 1, n}] /.
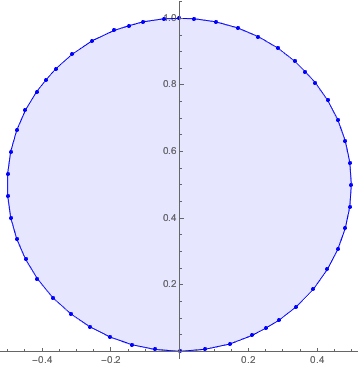
sol[[2]];Отобразить полученный результат на графике.
Show[ListPlot[rectpts, PlotStyle -> {Blue, PointSize -> Medium}],
Graphics[{Opacity[.1], Blue, EdgeForm[Blue], Polygon[rectpts]}],
AspectRatio -> 1, ImageSize -> Medium]
